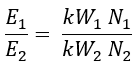The induction motor and transformer both are singly energized devices. The stator and rotor of an induction motor can be compared to the primary and secondary windings of the transformer. Similarly, from the e.m.f. equation of transformer we can derive the equations for EMF induced in the stator and rotor of the motor.
Thus, when a 3-phase supply is fed to the stator, a rotating field will be set up and emf's (E1 & E2) are induced in the stator and rotor.
Where kW1 and kW2 are winding factors for the stator and rotor windings respectively. Therefore,
The above expression is similar to the voltage transformation ratio of the transformer. The slight difference in these equations is due to the use of distributed winding for the induction motor as compared to the concentrated coils used in the transformer.
An induction motor at standstill exhibits the characteristics of a transformer on no-load. There also exist leakage fluxes in the induction motor as seen in the transformer. The behavior of both devices is similar to load conditions also.
Thus, we can say that the behavior of an induction motor is the same as that of a transformer. Therefore, the vector or phasor diagram of the induction motor can be developed similarly to that of a transformer. The phasor diagram is drawn on a per-phase basis.
Phasor or Vector Diagram of Induction Motor :
Let us take the mutual flux Φ between the stator and rotor windings as the reference phasor. This flux induces emf's in the stator and rotor. These emf's under running conditions are E1 and sE2 respectively lagging 'Φ' by 90°. Since the rotor winding is a short circuit, the voltage sE2 sets up the rotor current I2 lagging behind by an angle Φ2, and sE2 will be equal to the rotor impedance drop.
From the above, the phasor diagram of induction motor on load condition can be drawn as,
The current flowing in the stator winding i.e., stator current is,
Io = Io + I'2
Where- Io = No-load current of the induction motor.
- I'2 = Rotor current referred to the stator.
The phasor sum of E1, I1 R1, and I1 X1 gives the applied voltage V1 Cos Φ1 is the power factor of the stator and Cos Φ1 is the power factor of the rotor circuit.
