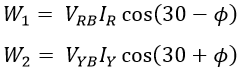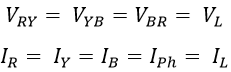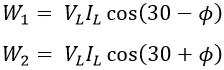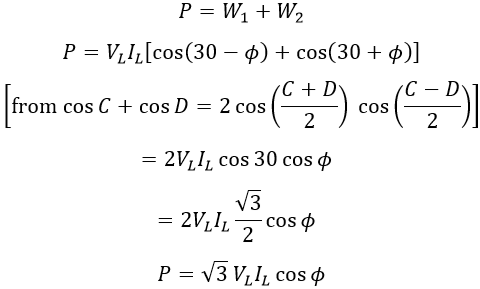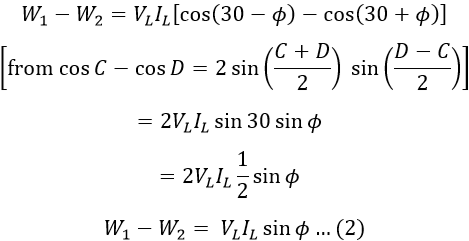In the last article, we have seen the two wattmeter method of measuring three-phase power with an unbalanced load. In this, let us see the two wattmeter method with a balanced load. In a balanced three-phase system total power consumed will be √3 VL IL cos Φ, this will be equal to the sum of the readings measured by the two wattmeters in two wattmeter method.
Two Wattmeter Method with Balanced Load Condition :
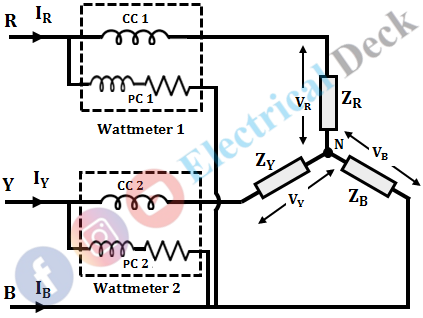
The connection diagram for two wattmeter method of measuring the three-phase power of balanced star connected load is shown below.
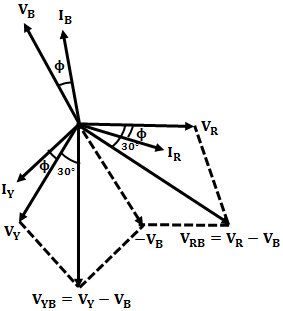
Let VR, VY, and VB and IR, IY, and IB be the RMS values of phase voltages and phase currents. If the load is to be considered inductive. The phase currents IR, IY, and IB lag behind the corresponding phase voltages VR, VY, and VB by an angle Φ. The phasor diagram of such a load with a power factor of cos Φ is shown below.
From the phasor diagram, the power measured by the two wattmeters W1 and W2 is given by, Since the load is balanced, for star-connected load, For balanced load condition, wattmeters readings will be,Therefore, the total power P consumed by the 3-phase balanced load will be the sum of two wattmeters readings, i.e.,
Measurement of Power Factor using Two Wattmeter Method :
From the above,W1 + W2 = √3 VL IL cos Φ ...(1)
Similarly,
Dividing equation 2 by 1, we get,
Therefore, power factor cos Φ is,
Let us see the variation of the wattmeter readings with the power factor.
At Unity Power Factor Lagging :
If the power factor of the load is unity i.e., cos Φ = 1. We get Φ = 0°. The power measured by the wattmeter-1 is,W1 = VL IL cos(30 - 0) = √3/2 VL ILSimilarly, power measured by the wattmeter-2 is,W2 = VL IL cos(30 + 0) = √3/2 VL IL
Hence, at unity power factor, both the wattmeters read half the value of total power consumed by the load i.e., both wattmeters read the same values.
At Half Power Factor Lagging :
If the power factor of the load is half i.e., cos Φ = 1/2. We get Φ = 60°. The power measured by the wattmeter-1 is,W1 = VL IL cos(30 - 60) = √3/2 VL ILSimilarly, power measured by the wattmeter-2 is,W2 = VL IL cos(30 + 60) = 0
Hence, at 0.5 power factor, only wattmeter 1 reads the total power i.e., only one wattmeter reads the value.
At Zero Power Factor Lagging :
If the power factor of the load is zero i.e., cos Φ = 0. We get Φ = 90°. The power measured by the wattmeter-1 is,W1 = VL IL cos(30 - 90) = 1/2 VL ILSimilarly, power measured by the wattmeter-2 is,W2 = VL IL cos(30 + 90) = -1/2 VL IL
Hence, at zero power factor, both the wattmeters indicate equal and opposite powers, so that their sum equals zero. Since wattmeter cannot show negative value as scale starts from zero.
In such conditions, the terminals of either the current or voltage coil of the wattmeter that reads negative must be interchanged (note - should not interchange the terminals of both coils). This causes the wattmeter to read positive values, but for calculations, we have to consider it as a negative value only.