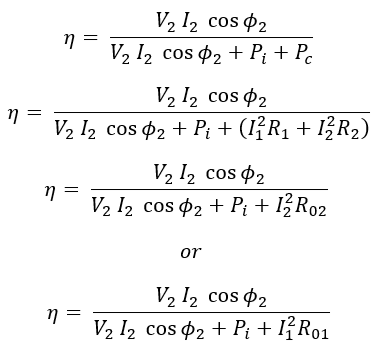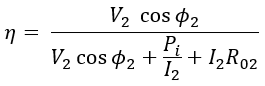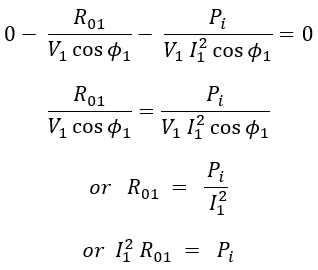It is important to calculate the efficiency of any device. The efficiency of a device determines the performance of how efficiently the device is operated i.e., the capability of a device to give any amount of output energy for given specific input energy. If both input and output values are the same then it can be said that the device is working at 100% (terms of %) efficiency.
Efficiency of a Transformer :
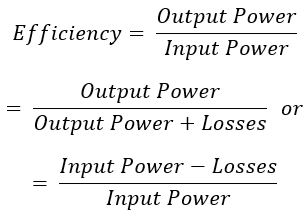
The efficiency of a transformer is defined as the ratio of output in watt (or kW) to input in watt (or kW), and is represented by the letter 'Ƞ' (and is also known as commercial efficiency). The expression is given by,
A transformer is a highly efficient device and has very small losses. The different losses that occur in a transformer are iron or core losses, copper losses, and stray losses. The stray loss of a transformer is comparatively very small and can be neglected.
Since the remaining losses are not constant, they will be different at different loads, and thus efficiency also varies with the variation of load on the transformer.
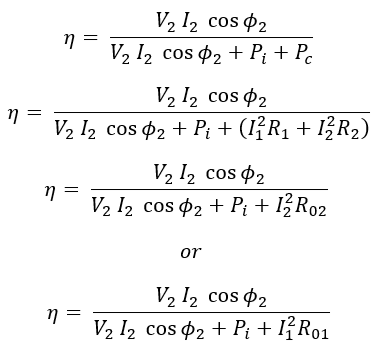
Where,- The iron or core losses Pi (sum of hysteresis loss and eddy current loss) in a transformer can be obtained from a no-load test. The core losses practically remain constant if the input voltage is constant.
- The copper losses Pc can be calculated by performing a short-circuit test on the transformer. These losses vary as the square of the load current.
- V2 = Secondary terminal voltage.
- I1 = Primary winding current.
- I2 = Secondary load current.
- Cos Φ2 = Power factor of the load (for purely resistive load it is 1).
- R1 & R2 = Primary and secondary winding resistance.
- R01 = Total resistance referred to the primary side.
- R02 = Total resistance referred to the secondary side.
Taking the above equation,
Where,- R02 = R2 + R1 K2
- I22 R02 = Total copper loss in the windings
Dividing with I2 on both numerator and denominator. we get,
Since the secondary voltage V2 is kept almost constant for every transformer. For efficiency to be maximum for a particular power factor the denominator should be minimum.
Condition for Maximum Efficiency of a Transformer :
To determine the condition of the load on the transformer at which the efficiency would be maximum. Let,- Primary input = V1 I1 Cos Φ1
- Iron loss = Pi
- Copper loss = I12 R01 or I22 R02
For efficiency to be maximum, the above equation should be differentiated with respect to I1 and equating it to zero.
Hence the efficiency will be maximum when variable or copper loss (I12 R01 or I22 R02) are equal to constant or iron or core losses (Pi). The current I2 corresponding to the maximum is given by,
Similarly, the kVA corresponding to maximum efficiency is given by,