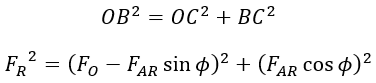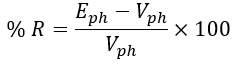Rothert's MMF Method or Ampere-Turn Method of finding voltage regulation of alternator is the converse of the EMF method. In a synchronous generator or alternator, the MMF is due to field ampere-turns (i.e., the product of field current and number of turns in field winding). The terminal voltage produced by field MMF of the alternator is the vector sum of the following,
- The MMF necessary to induce rated terminal voltage by the field ampere-turns on no-load. This can be obtained by performing the open-circuit test on the alternator.
- The MMF produced by field ampere-turns has to overcome the demagnetizing effect of armature reaction and impedance drop to produce full-load current when the alternator is loaded. This value is obtained by a short-circuit test.
Here, we can see that similar to EMF or synchronous impedance method, the MMF method also utilizes data obtained from O.C. and S.C. tests. In this method, when the alternator is loaded change in terminal voltage due to armature leakage reactance is replaced by the additional armature reaction MMF, and combined with the existing armature reaction MMF. So that the entire drop in the alternator is due to armature reaction MMF.
In an alternator under short-circuit condition the impedance drop i.e., due to armature resistance and armature leakage reactance is usually very small and can be neglected.
Hence in a short-circuit test, to circulate full-load current, the MMf by field ampere-turns has to overcome the drop due to the armature reaction effect only. Therefore under short-circuit condition the power factor of such a purely reactive circuit with an armature reaction effect is almost zero lagging.
We know that the at lagging p.f. the armature reaction effect is wholly demagnetizing. Thus the field MMF required to produce a full-load current has to overcome the armature reaction effect which is entirely demagnetizing in nature.
The above figure shows the field MMF required to induce rated terminal voltage under open-circuit condition FO, and field MMF required to circulate full-load current under short-circuit condition FAR.
Phasor Diagram of MMF Method :
Let us consider when the load power factor has any value, either lagging or leading. Then the resultant MMF is determined by vector addition of FO and FAR.
For Lagging Power Factor :
The below shows the phasor diagram at lagging power factor i.e., the phase current Iaph lags the phase voltage Vph by an angle cos Φ. Here the rated terminal voltage of open-circuit test Fo lies at a right angle to Vph. Since the armature reaction is due to the armature current Iaph, the component FAR lies in phase with the current Iaph.
Since the field MMF has to overcome the armature reaction effect to produce rated terminal voltage. The resultant field MMF FR is obtained by taking -FAR vectorially to FO as shown above. From the triangle OCB,
- AC = FAR sin Φ
- BC = FAR cos Φ
Therefore,
For Leading Power Factor :
Similarly, the phasor diagram if the load power factor is leading, where phase current Iaph leads the phase voltage Vph is shown below. The resultant FR is obtained by adding -FAR to FO.
From the triangle OCB,- AC = FAR sin Φ
- BC = FAR cos Φ
Therefore,
Regulation Calculation :
From the above two equations, the resultant field MMF FR at any load power factor is determined. Therefore, the required induced emf Eph to get rated terminal voltage Vph is plotted corresponding to FR on O.C.C. characteristics.
By knowing the value of Eph the regulation can be obtained as,
Note :
It should be noted that the regulation of alternator calculated from MMF or ampere-turn method is lower than the actual value at working conditions. Hence, this method is also referred to as the 'Optimistic Method'.