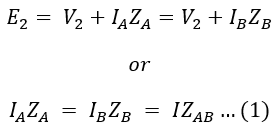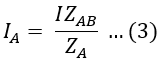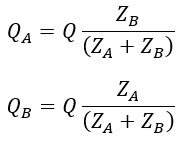Parallel Operation of Single Phase Transformers

In the last article, we have seen the reasons and conditions for the parallel operation of two or more transformers. Now let us see the parallel operation of single-phase transformers and how the load is shared among them.

Load Sharing by Two Transformers :

Let us consider two transformers A and B are connected in parallel to the supply bus (primary) and load bus (secondary) as shown below. Similarly, two or more transformers can be connected in parallel depending upon the increase in load demand.

Let us summarize the conditions for satisfactory parallel operation of single-phase transformers,

• The transformers should be suitable for the supply system voltage and frequency.
• The polarity of the transformer should be ensured that properly connected.
• Transformation or turn ratios of the transformers should be the same.
• The percentage (per-unit) impedance of the transformers should be the same.
• The transformer's ratios of resistance to reactance should be the same.

For satisfactory parallel operation, the transformers must meet the above conditions. Otherwise, under the no-load condition, the localized circulating current will be produced due to unequal induced EMFs in the secondaries to equalize the voltage in each transformer.

Thus when the two transformers have loaded this results in an unequal share of the load with respect to their full kVA output and cause another transformer to overload. The equivalent circuit of the two transformers with unequal induced EMFs is shown below.

However, it is difficult in practice to build such identical transformers. In order to reduce the circulating current, the difference between the voltage ratios of the transformers should be least as possible. This is possible when the difference between the magnetizing current of the transformers is very small.

The circulating current will cause undesirable effects like,

• The full kVA output of the transformers cannot be utilized to a full extent.
• It overloads one transformer from the parallel connected group.
• The copper losses in the transformer's windings increases.

With Equal Voltage Ratio :

When two transformers operating in parallel having equal voltage ratios (i.e., E₁ = E₂ = E), the total load current will be divided between them inversely as their equivalent impedance. Since the voltage ratios are the same if we neglect magnetizing currents of two transformers the equivalent circuit referred to as secondary is represented as shown below.

Let,

• Z_A & Z_B = Impedances of the transformers A and B respectively.
• I_A & I_B = Currents supplied to the load from transformers A and B respectively.
• V₂ = Common terminal load voltage.
• I = Combined load current
• V₁ = Common supply input voltage.

From the above circuit, the voltage equation may be written as,

Where Z_AB = combined impedance of Z_A and Z_B. Since both are in parallel the equivalent impedance is given by,

From equation (1), I_A is given by,

Substituting the value of Z_AB from equation (2) in equation (3),

Similarly, I_B is given by,

Multiplying on both sides by V₂ × 10^-3 we have,

Let,

• Q = V₂ I × 10^-3 = The combined load kVA
• Q = V₂ I_A × 10^-3 = kVA carried by transformer A
• Q = V₂ I_B × 10^-3 = kVA carried by transformer B

If the ratios of resistance to reactance are not equal the power factors of the transformers A and B will be different and the expression for kVA supplied will remain the same. Hence, there must be an inverse relationship between the kVA carried and the impedance of the transformer to share the load to its full kVA output without overloading.

The phasor diagram of the transformers operating in parallel with their quantities is shown below.