Field Test of DC Series Motor - Advantages & Disadvantages

Generally, Swinburne's test is the most popular testing method of dc machine to determine losses and efficiency. It is an indirect method of testing a dc machine performed without actually loading the machine. Since it is a no-load test, a series motor at no-load attains dangerously high speed. Hence, it is difficult to perform Swinburne's test on large series motors.

Therefore, Swinburne's test is only applicable for dc shunt and small series machines. This drawback can be overcome by performing field test. In this article let us see how the efficiency of dc series motors can be determined by conducting a field test.

Field Test of DC Series Motor :

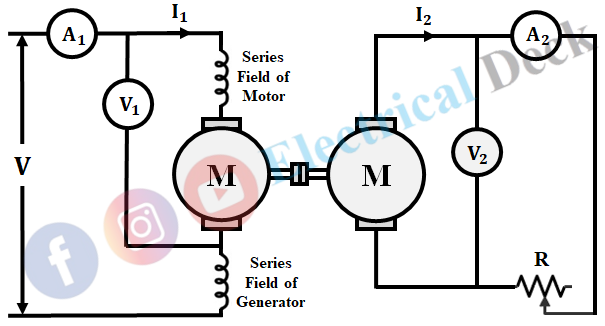
A field test uses two similar dc series motors, which are mainly used for electric traction works. In fields test, two similar dc series motors with their field windings connected in series are used to determine losses and efficiency.

The two machines are coupled mechanically in which one runs as a motor and the other as a generator driven by the motor. The electrical output from the generator is passed through variable load resistance R and dissipated as heat. The circuit diagram for fields test on dc series motor is shown below.

As they are rotating they have frictional losses and constant losses. The iron and frictional losses of the two are made equal by,

• Exciting the machines equally, which is achieved by joining the series field winding of the generator with the motor armature circuit.
• Synchronizing the machines by running them at equal speed.

Copper and iron losses depend upon B_m and frequency which in turn depends upon B_m flux and speed. Thus the iron losses can be maintained constant by satisfying the above two conditions. Load resistance R is varied till the armature connected in the motor armature circuit reads the full-load value. After this adjustment, different ammeter and voltmeter readings are noted.

Let,

• Supply voltage = reading of voltmeter, V = V₁ volts
• Motor input current = reading of ammeter, A₁ = I₁
• Terminal voltage of generator = readings of voltmeter, V₂ = V₂
• Loading current of generator = reading of ammeter, A₂ = I₂
• Armature resistance of each machine = R_a
• Series field of each machine = R_se
• Input to the whole set = V₁ I₁
• Output of the whole set = V₂ I₂
• Total losses of the set = P₁ = V₁ I₁ - V₂ I₂
• Series field and armature copper loss of motor = (R_a + R_se) I₁²
• Series field and armature copper loss of generator = I₂² R_a + I₁² R_se

Total copper losses of the set,

P_cu = I₁² R_a + I₁² R_se + I₂² R_a + I₁² R_se

P_cu = I₁² (R_a + 2R_se) + I₂² R_a

Stray losses for the set = P_T - P_cu Stray losses for each machine = (P_T - P_cu) / 2 = P_s

Motor Efficiency :

• Motor input = V₁ I₁
• Motor losses = I₁² (R_a + R_se) + P_s
• Motor output = V₁ I₁ - [I₁² (R_a + R_se) + P_s]

Therefore, the efficiency of motor is,

Generator Efficiency :

• Generator input = V₂ I₂
• Generator losses = I₂² R_a + I₁² R_se + P_s
• Generator output = V₂ I₂ + I₂² R_a + I₁² R_se + P_s

Therefore, the efficiency of generator is,

Advantages of Field Test :

• Since the excitation and speed of the two machines are same, determination of stray losses is easy.
• The generator armature is connected to load resistance R directly without any switch so that the load is not thrown off accidentally.
• Since the motor and generator fields are in series, the iron losses in both machines are same.

Disadvantages of Field Test :

• The setup is bulky, which requires a lot of space.
• Since two machines are used, there will be an increase in the consumption of energy.
• The electrical output from the generator is dissipated through load resistance in the form of heat. In the case of Hopkinson's Test, it is used as feedback to the motor.