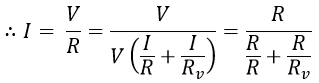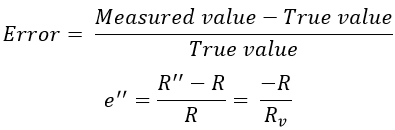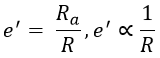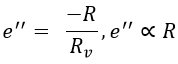Based on the value of resistance, the resistances are classified as low (<1Ω), medium(1Ω to 100kΩ), and high (>100kΩ) resistance. There are various methods used for measuring resistance based on their classification.
Among these methods, the ammeter-voltmeter method is one of the methods used for measuring low and medium values of resistance. Let us see the measurement of resistance using the ammeter-voltmeter method.
This method is the simplest of all, as it requires an ammeter and a voltmeter which will be easily available in the laboratory. Also, the connections are very simple and there is no lengthy procedure for the measurement of resistance.
The ammeter, as usual, will be connected in series and the voltmeter in parallel. The ratio of the voltmeter to ammeter reading will give the value of resistance under measurement. Based on the relative connections of the ammeter and voltmeter with respect to the unknown resistance there are two methods.
Ammeter Connected to the Side of Unknown Resistance :
The below shows the connections for measuring unknown resistance when the ammeter is connected in series with it.
Let,- V = Voltmeter readings
- R = Unknown resistance
- I = Ammeter readings
- Va = Voltage across ammeter
- VR = Voltage across unknown resistance
- R' = Measured value of resistance with the above connections
- Ra = Internal resistance of ammeter.
In the above circuit, since the ammeter is directly in series with R, the ammeter readings indicate the current through R. The voltmeter is not in parallel with R, rather it is connected in parallel with the series combination of unknown resistance and the ammeter.
Therefore, voltmeter reading,V = VR + VaWhere, VR = IR, Va = IRa.V = IR + IRaV = I(R + Ra)Therefore, measured value of resistance,
From the above equation, the measured value is not equal to the exact value or the true value of the unknown resistance. This is because of the inherent resistance of the ammeter. The internal resistance of the ammeter or any device cannot be made equal to zero, hence always there exist an error in the measured value of resistance. The amount of error is given by,
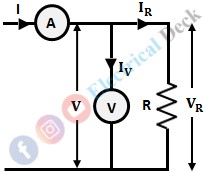
Voltmeter Connected to the Side of Unknown Resistance :
The below shows the connections for measuring the unknown resistance when the voltmeter is connected to the side of the unknown resistance.
Let,- V = Voltmeter readings
- R = Unknown resistance
- I = Ammeter reading
- IR = Current through unknown resistance
- VR = Voltage across unknown resistance
- Iv = current through voltmeter
- R'' = Measured value of resistance with the above connections
- Rv = Internal resistance of voltmeter.
In the above circuit, the voltmeter is connected directly in parallel with the unknown resistance, whereas the ammeter is in series with the parallel combination of voltmeter and R. The voltmeter reads the voltage across R, but the ammeter reads the sum of currents through R and voltmeter.
Therefore, voltmeter reading,I = IR + IvWhere, IR = V/R, Iv = V/Rv.Therefore, the measured value of resistance,
From the above equation, the measured value of resistance is not equal to the true value of the unknown resistance, hence there exists an error. This is because of the internal resistance of the voltmeter and hence cannot be made equal to infinity. The amount of error is given by,
Condition for the Selection of Circuit :
From the equation of error when the ammeter is connected to the side of unknown resistance,
The error is inversely proportional to the value of unknown resistance i.e., the higher the value of R, the lesser will be the error. Hence connection (1) can be used for measuring the high value of resistance so that, the error is small and the accuracy is more.
From the equation of error when the voltmeter is connected to the side of unknown resistance,
The error is directly proportional to the value of unknown resistance, i.e., lesser is the value of R, lesser will be the error. Hence connection (ii) should be used for the measurement of low-value resistance in order to have greater accuracy.
The measurement of low resistance is not suitable using the Voltmeter-Ammeter method because it is highly inaccurate. The inaccuracy of the measurement is due to the inaccuracy of the ammeter and voltmeter.
We know that nothing is ideal in this world and hence each instrument has got its own accuracy. The inaccuracy of the voltmeter and ammeter together will cause a large value of error in the readings. This error will become significant while measuring low-value resistance.
The main cause for the error in the readings is the voltage drop across the internal resistance of the ammeter and the shunting effect of the voltmeter. Even, if corrections are made, the error cannot be reduced to a great value.
This is because the internal resistance of the ammeter and voltmeter cannot be made equal to zero because resistance is the property of the material itself.