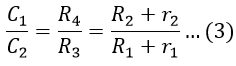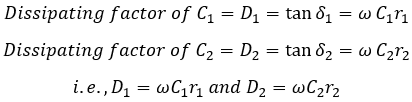Desauty's bridge is the simplest ac bridge circuit used for the measurement of unknown capacitance. The bridge gives a fair degree of accuracy for measuring capacitance over a wide range. It can be also used for comparing two capacitance.
Construction & Theory of Desauty's Bridge :
The bridge consists of four branches or arms. Two capacitors C1 and C2 are placed in branches AB and AD respectively. The branches BC and CD consist of resistors R3 and R4 respectively. An ac source is connected between terminals A and C. The circuit diagram of the bridge is shown in the below figure.
A null indicator is connected across terminals B and D, which indicates null deflection when the bridge is balanced.
Let,- C1 = Unknown capacitance
- C2 = Known standard capacitance
- R3 = Known standard non-inductive resistance
- R4 = Known standard non-inductive resistance.
From the above figure, the impedances in each arm is given as,
When the bridge is balanced, we have,
It is the easiest method for the measurement of capacitance as it has a simple circuit and only one variable element. In order to bring the bridge into a balanced condition, either R3 or R4 can be chosen as a variable element. The below shows the phasor diagram for Desauty's bridge.
The above equation holds good only when ideal capacitors (i.e., lossless capacitors) are used. This method is useful only to measure the capacitance of lossless capacitors. If either of (or both) the capacitors is imperfect, then the balance can never be achieved by varying R3 or R4. This drawback can be overcome by modified Desauty's bridge.
Modified Desauty's Bridge :
The modified Desauty's bridge is used for the measurement of unknown imperfect capacitance. It is the modification of Desauty's bridge. Imperfect capacitance is those which contain dielectric losses. The circuit diagram of the bridge is shown below.
In modified Desauty's bridge, the two capacitors C1 and C2 are connected in series with two resistors R1 and R2. To measure capacitance with dielectric losses another two resistors r1 and r2 are connected to the two capacitors that give the loss component of their respective capacitor.
Let,- C1 = Unknown imperfect capacitance
- C2 = Known standard capacitance
- R1, R2, R3, R4 = Known variable non-inductive resistances
- r1, r2 = Resistances having loss component of two capacitors.
From the above figure, the impedances in each arm is given as,
When the bridge is balanced, we have,
Equating real terms on both sides, we get,
Equating imaginary terms on both sides, we get,
Comparing equations 1 and 2, we get,
The balanced condition in modified Desauty's bridge is determined by changing the resistances R1, R2, R3, and R4 in the circuit. The dissipating factor D of the two capacitors are,
Simplifying equation 3, we get,
Also from equation 3, we have,
In the above equation, if one of the dissipation factors is given, the other dissipation factor can be determined. One of the disadvantage of this method is that the dissipation factor is not precise and accurate because the differences in their resistance quantities (i.e., R1 R4/R3 and R2) are very small.
Hence, the difference is not highly accurate and so the dissipating factor (D) is not used for accurate measurements. The phasor diagram of the modified Desauty's bridge under balance conditions is shown in the figure below.