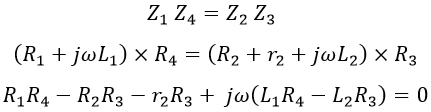Maxwell's Bridge - Circuit, Types, Equation, Phasor Diagram and Advantages

The Maxwell’s bridge or Maxwell’s Wein bridge is an AC bridge used to find or measure the unknown self-inductance. There are different types of ac bridges used for the measurement of self-inductance in which Maxwell’s bridge is the most commonly used bridge.

The bridge uses the principle of null-deflection i.e., by balancing the impedances on the bridge arms. The equation obtained when the bridge is balanced (i.e., ratio of impedances are balanced) can be used to determine the unknown inductance connected to it.

There are two types of Maxwell's bridges used to find unknown inductance,
Maxwell’s inductance bridge
Maxwell’s inductance capacitance bridge.

Maxwell’s Inductance Bridge :

In Maxwell's inductance bridge the unknown self-inductance to be measured is compared with the known inductance. Hence the unknown self-inductance and internal resistor of an inductor can be measured with Maxwell's inductance bridge. The circuit diagram is shown in the below figure.

Let,
L₁ = Unknown inductance to be measured
R₁ = Resistance of the Unknown inductance
R₃, & R₄ = Standard non-inductive resistances
R₂ = Standard Variable resistance
L₂ = Standard Variable inductance with fixed resistance r₂.
From the above figure, the impedances of the respective arms are given as,
Under balanced condition (i.e., when detector shows null deflection), we have,
On equating the real and imaginary parts on both sides, we get,
Hence, the unknown self-inductance and resistance of the inductor are obtained in terms of known standard values. Also, both the equations are independent of frequency term.

Phasor Diagram of Maxwell’s Inductance Bridge :

In Maxwell's inductance bridge, the resistance R₂ is the decade resistance box. The resistor R₃ and R₄ can have their values as from 10, 100, 1000, and 10,000 Ω by the successive adjustment of L₂ and R₂. The balance of the bridge can be adjusted. The phasor diagram of Maxwell's inductance bridge under balance condition is shown below.

Maxwell’s Inductance Capacitance Bridge :

Maxwell’s inductance capacitance bridge is also similar to Maxwell’s inductance bridge seen above. But here the unknown self-inductance to be determined is compared with the standard known capacitor. The circuit diagram for Maxwell’s inductance capacitance bridge is shown in the below figure.

The advantages of using a standard capacitor in Maxwell's bridge are as follows,
The standard capacitors used in Maxwell's bridge are of low cost compared to the stable and accurate standard inductors.
These capacitors are small in size.
The capacitors used in this bridge are lossless capacitors as there is less possibility of losing energy.
The capacitor is independent of the external fields. Whereas, the stray magnetic fields can be eliminated by providing proper shielding on the standard inductor.
In Maxwell's inductance bridge, there is a requirement of adjusting the current flow through the inductor to show the rated value of inductance.
Let,
L₁ = Unknown inductance to be measured
R₁ = Resistance of the unknown inductor
R₂, R₃ = Standard non-inductive resistances
R₄ = Standard non-inductive variable resistance
C₄ = Standard variable capacitor.
From the above figure, the impedances of the respective arms are given as,
Under balanced condition (i.e., when detector shows null deflection), we have,
Equating the real and imaginary terms on both sides, we get,
Thus, the bridge can be balanced by varying R₄ and C₄. The Q-factor or storage factor of the inductor is given by,

From the above expression for Q factor obtained from Maxwell's inductance capacitance bridge. The value of the Q factor is proportional to the product of R₄ and C₄. We know that, usually, the value of C₄ will be in μF or pF.

In order to have a greater value of Q factor, R₄ must be in megaohms or greater than that, so that the product is high. Resistance of such a high value is very difficult to obtain and also very costly. Hence, the measurement of inductance using Maxwell's inductance-capacitance bridge is limited to low range values of Q i.e., between 1 and 10. Hay's bridge is used for high Q factor coils.

The below shows the phasor diagram for Maxwell's inductance capacitance bridge.

Also, from the equations of L₁, it is clear that L₁ is the product of R₂, R₃, and C₄. The value of C₄ is usually in μF. Now if the value of R₂ and R₃ is selected such that R₂ R₃ is 10⁶ then L₁ = 10⁶ × C₄ × 10^-6 = C₄. Hence, the dial of the variable capacitor C₄ will directly give the value of inductance.

Advantages of Maxwell's Bridge :

The calculated values of R₁ and L₁ are independent of C₄ and R₄ respectively. Hence, there is no effect on R₁ and L₁ by choosing R₄ and C₄ as variable elements.
The stray magnetic fields do not disturb the balance, as the variable element used here is the capacitor.
The balance equations do not contain the frequency terms and hence the fluctuations in frequency do not disturb the operation or balancing of bridge.
As both R₁ and L₁ depend upon the product of R₂ and R₃, their product can be adjusted conveniently for any inductance value.
Calculation of Q-factor is very simple and easy.
Very wide range of inductance can be measured not only at power frequencies but also at audio frequencies.

Disadvantages of Maxwell's Bridge :

The use of a standard variable capacitor makes the bridge highly expensive. However, this can be overcome by using a fixed capacitor and varying R₄ and an additional resistor in series with the inductance to be measured.
The bridge is limited for the measurement of medium Q coils only i.e., Q value between 1 and 10.

Applications of Maxwell's Bridge :

Maxwell's bridges are widely used to measure the self-inductance of the coil because balance equations are independent of the supply frequency.
These are also commonly used in Q-meters to measure the quality factor of the inductors.
It measures inductance at audio and power frequencies.