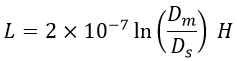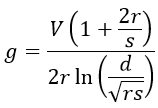In transmission lines, we require high voltages and power for transmission over long distances, so as to meet their high voltage requirements we need to supply huge power. But due to the high voltages i.e., greater than 230 kV, corona occurs resulting in huge power loss and if there is only one conductor per phase then its interaction with communication lines is very high and uncontrollable.
So, for extra-high voltages, there should be two or more conductors per phase with very little spacing between them such that the high voltage gradient is minimized. When a line has two, three, or more conductors, it is known as bundled conductors.
For bundled conductors, unless and until there is an interchange of the conductors within the bundle, the current is not distributed equally among the conductors of the bundle. The spacing between the sub-conductors in a bundle of one phase is normally 40cm.
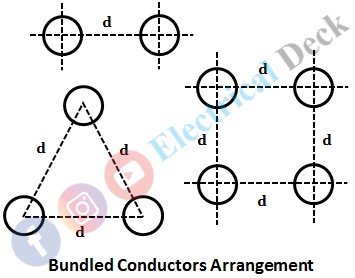
Bundled conductors consist of two or more conductors per phase, placed at a constant distance from each other. There are different configurations of bundled conductors depending on the number of sub-conductors per phase.
In a three-conductor bundle for each phase, the conductors are arranged in an equilateral triangle manner i.e., at the corners of the equilateral triangle. While in a four-conductor bundle it is arranged in square shape.
If there are two sub-conductors per phase then it is called a duplex arrangement. If there are three sub-conductors per phase, it is called the triplex arrangement. If there are four sub-conductors per phase, it is called a quadruplex arrangement. Below shows the duplex, triplex, and quadruplex arrangements of bundled conductors.
Role of Bundled Conductors in Transmission Lines :
Almost all the high voltage and extra high voltage transmission networks use bundled conductors to transmit power due to the following reasons,
Reduced Surge Impedance :
By increasing the number of conductors of a single-phase, automatically the distance of the phase in which the conductors are placed increases, and the GMD of that phase increases i.e., self GMD or GMR increases.
We know that inductance per phase is given as,
Where,- Ds = Geometric mean radius (GMR) or self GMD
- Dm = Geometric mean distance (GMD).
If Ds is the GMR of each sub conductor and d is the bundle spacing, the GMR of the bundled conductor is,
From the equation of inductance per phase, the inductance is inversely proportional to self GMD. So when self GMD increases, inductance decreases, and thus surge impedance which is given as √(L/C) is reduced. As a result, bundling of conductors minimizes surge impedance.
Reduced Reactance :
Similarly when self GMD of the conductors is increased by bundling of conductors, undoubtedly the reactance becomes less as reactance of a conductor is inversely related to self GMD or GMR i.e.,
Hence, a decrease in the reactance by increasing self GMD of the bundled conductor effect in the increase in the net surge impedance loading, the capacitance of the line, and loading capability.
Reduced Corona Loss :
When more conductors are used, spacing between the sub-conductors is more due to which the potential gradient decreases. Due to this decreased potential gradient, the voltage at which corona occurs is increased. Hence, the corona will occur at a greater voltage due to the bundling of conductors thereby reducing the corona loss. The gradient of a conductor is,
The gradient of a conductor is inversely proportional to spacing. So, the voltage gradient is minimized, and by this interference between the lines is also reduced.