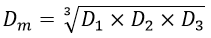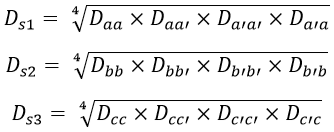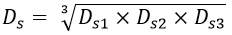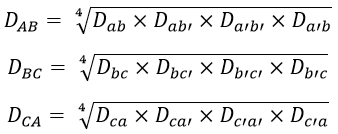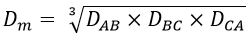The inductance and capacitance calculations of an overhead transmission line are simplified by using two important terms namely GMR (self GMD) and mutual GMD. Particularly, when there is a multiconductor arrangement, GMR and GMD ease the inductance and capacitance solving process.
GMR (self GMD) :
GMR stands for Geometrical Mean Radius. It is also called the self GMD (Geometrical Mean Distance) It is represented by Ds. We know that the expression for the inductance per conductor per meter is given by,
The term (0.5 x 10-7) in the above equation represents the inductance due to the flux which is present inside the conductor. Hence, the above equation can be simplified by introducing GMR that eliminates the term (0.5 x 10-7). This can be done as follows.
The solid conductor can be replaced by an equivalent hollow conductor whose surface is extremely thin. As the ac current flows through the surface, the internal conductor flux linkage becomes zero. This eventually reduces the internal flux to zero and the term (0.5x 10-7) gets eliminated.
In order to compensate for the absence of the internal flux linkages by allowing space for additional flux, the radius of the equivalent hollow conductor is chosen such that it is smaller than the physical radius of the solid conductor. If 'r' is the radius of the solid conductor, then mathematically it is proved that GMR is equal to 0.7788 x r. Thus above equation reduces to,
In the above equation, Ds = self-GMD or GMR = 0.7788r. GMR depends upon the shape of the conductor and the size of the conductor. GMR is independent of spacing between the conductors.
Mutual GMD :
GMD stands for Geometrical Mean Distance and is denoted by Dm. The introduction of the term mutual GMD simplifies the mutual inductance calculations between the spaced conductors.
Actually, the mutual GMD represents the geometrical mean distance from one conductor to the other. It also represents the equivalent geometrical spacing. GMD for a different arrangement of conductors has different values.
GMD of Two Adjacent Conductors :
If two conductors are placed adjacent to each other and if the spacing between them is much greater than the diameter of the conductor then, the mutual GMD is equal to the distance between their centers. Therefore, mutual GMD, Dm = Spacing between conductors = D.
3-Phase Single Circuit Line :
For a 3-phase single circuit line, the mutual GMD is equal to the equivalent equilateral spacing. Therefore, mutual GMD is given as,
3-Phase Double Circuit Line :
Consider a 3-phase double circuit line with the arrangement of conductors as shown in the figure.
In the figure above, the conductors a,b, and c belong to the first circuit, and a', b', and c' belong to the other circuit. Now, GMR (self GMD) of each conductor = 0.7788 x r, the self GMD of the combination of aa', bb', and cc' is,
Where,- Daa = Da'a' = Dbb = Db'b' = Dcc = Dc'c' = Self GMD of conductor
- Daa' = Da'a = Distance between a and a'
- Dbb' = Db'b = Distance between b and b'
- Dcc' = Dc'c = Distance between c and c'.
Therefore, the equivalent self GMD per phase is given by,
Now mutual-GMD between the phases AB, BC, and CA is,
Therefore, the equivalent mutual GMD is given by,
GMD depends upon the spacing between the conductors. It is independent of the shape of the conductor, size of the conductor, and orientation of the conductor.