Ungrounded Neutral System - its Behaviour & Disadvantages

The ungrounded neutral system is a neutral system in which there is isolation between neutral and ground i.e., there is no electrical connection between neutral and ground. Hence the ungrounded neutral system is also called an isolated neutral system or free neutral system or insulated neutral system.

Ungrounded Neutral System :

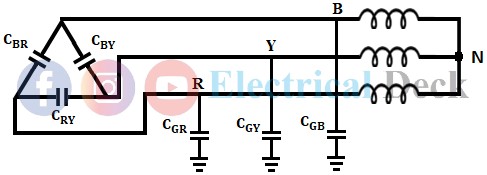
A simple 3-phase system with ungrounded is shown in the below figure. In reality, there exists a capacitive effect between one conductor to another and the line conductors also have a capacitance effect with the ground too. Thus capacitive currents flow in all the phases of the system.

In the above figure, the capacitors between conductor and ground are star-connected, whereas the capacitors between each conductor are delta connected. The capacitance value of the delta-connected capacitors can be neglected as they have no effect on the earth circuit.

During Normal Condition :

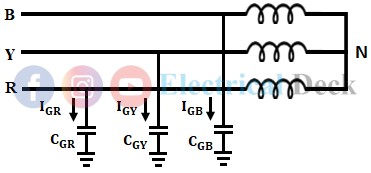
In normal operating conditions, the system is balanced and the capacitances to the ground are assumed to be equal i.e., C_GR = C_GY = C_GB = C_EC, where C_EC is the capacitance of each capacitor to ground. From the above figure, it was said that the delta-connected capacitors can be neglected as they have no effect on earth, if so done then the figure above gets modified as shown in the below figure.

As the capacitance becomes equal in every conductor then the phase voltages also become equal (in magnitude) i.e., V_GR, V_GB, V_GY, and hence the capacitance currents also become equal to V_ph/X_c.

V_CR = V_CB = V_CY (magnitudinally)

I_GR = I_GY = I_GB = V_ph/X_c

Under the normal operating conditions, the system is balanced i.e., all the line phase voltages will be equal in magnitude and have a phase difference of 120°. As the shunt capacitors of all the phases are the same, the corresponding charging current will also be equal. The currents will be equal in magnitude and have a phase difference of 120° as the system is balanced. Hence, the sum of these currents will be equal to zero.

i.e., I_R = I > 0

I_Y = I > -120°

I_B = I > -240°

∴ I_R + I_Y + I_B = 0

We know that, the neutral current is,

∴ I_N = I_R + I_Y + I_B = 0

Hence, there is no current flowing through the ground and therefore, the neutral and ground will be at the same potential under normal operating conditions.

During Fault Condition :

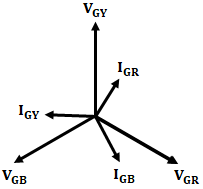
Let us assume that an L-G fault occurs on the system at some point F with the L-G fault in R, the potential of the R phase gets equal to ground potential, and due to this a short-circuit occurs in capacitance of line (i.e., C_GR). Therefore no current flows through C_GR.

The capacitive currents I_GB and I_GY flow through the phase lines B and Y respectively. The driving voltages of I_GB and I_GY are V_GB and V_GY respectively, moreover note is to be taken that V_RY and V_RB are line voltages. The two currents flowing i.e., I_GY and I_GB are having capacitive paths. Thus I_GY leads V_RY by π/2 and I_GB leads V_RB by π/2. The fault current I_F in R is nothing but the sum of the two currents I_GB and I_GY.

So under an earth fault in phase R,

Since phase voltages are equal, say equal to V_ph, and capacitances from line-to-ground are equal, say equal to X_C. So capacitive currents of healthy passes (I_GB and I_GY) under fault conditions become √3 times their respective values under healthy conditions. Therefore, the fault current I_F is nothing but the phasor sum of currents I_GB and I_GY.

Where, I_c is the charging current under normal conditions hence the capacitive fault current I_F becomes 3 times the normal per phase capacitive current. As the capacitive fault current is small in magnitude with which it can't operate protective devices. Hence, the ungrounded neutral system is not so efficient in providing protection against earth faults.

Disadvantages of Ungrounded Neutral System :

The effects of ungrounded neutral on system performance are,

• In an ungrounded system, the phenomenon of arcing grounds due to earth faults commonly occur and due to arcing grounds, there may be insulation breakdown.
• Due to arcing grounds in an ungrounded system, a temporary fault can shift into a permanent fault.
• When an earth fault occurs in an ungrounded system, then there will be an increase in the voltage of the healthy phases above the earth by √3 times its normal value, due to which the insulation of all machines and equipment connected to the system will experience severe stress.
• The ungrounded system cannot be provided with adequate protection as in this system the earth fault cannot be sensed easily. As the fault current will not be sufficient to initiate the operation of the protective relay. Hence, the earth fault relay in this system is more complicated.
• The capacitive current in the faulty phase of an ungrounded system will rise to 3 times that of the normal per phase capacitive current.
• In an ungrounded system, the overvoltages due to induced static charges and lightning surges will not be discharged to the ground and will be remaining in the system itself because of which the system equipment may get damaged.
• The actual fault location in an ungrounded system cannot be located. As in this system during an earth fault, the capacitive current in each phase will become unstable, as these capacitive currents will be contributing to the fault current. Because of an unbalanced capacitive current, it is not possible to install a discriminative type of fault indicator, but a neutral discriminative indicator can be connected across this type of system which will only give a warning on the occurrence of an earth fault without indicating the actual fault location.

Due to these disadvantages, the ungrounded system is not being used in the modern 3-phase system.