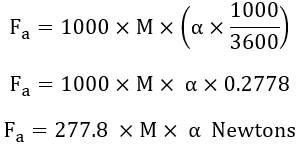What is Tractive Effort?
The effective force which is necessary to propel the train at its wheels is known as Tractive Effort. The tractive effort required can be defined or given in two situations, one is in level track and the other in inclined track. When the train is moving on a level track, then the acceleration due to gravity will be zero. Therefore on leveled track, the tractive effort required is given by,
When tractive effort is considered on an inclined track, the train possesses acceleration due to gravity and it is considered. Therefore the tractive effort required will be,
When the train is moving upwards or on elevation, then a positive sign is taken into consideration and when it is moving downwards, a negative sign is considered. In the above expression Fa represents the force required for giving acceleration to the train, Fg represents the force required to overcome acceleration due to gravity, Fr represents the force required to overcome the resistance of the train.
From the above equation, we can observe that tractive effort exerted by the train has to perform the following functions,- To give necessary linear and angular acceleration (Fa) to the train.
- To overcome the gravity component (Fg) of the weight of the train.
- To overcome the wind and frictional resistance (Fr) of the train.
Tractive Effort Required for Acceleration :
Consider a train at a standstill position that possesses the weight of M tones and which is to be accelerated with linear acceleration α, then the tractive effort is given by,
Where M is the dead weight of the train in tonnes and α is the acceleration in kmphps. The mass of the train in kg is 1000M and acceleration (α) in m/s2 is α × (1000/3600). Therefore on substituting M (in kg) and α (in m/s2) values in the above equation, tractive effort Fa, required for acceleration is given as,
When the train is in motion the rotating parts like wheels, armature, axles, etc., are also in motion whose effective mass is than its stationary mass and is given by Me. Therefore tractive effort Fa, is given as,
Fa = 277.8 × Me × α Newtons
Tractive Effort Required to Overcome Gravity :
When the train is considered on an inclined track moving upwards, then the train possesses acceleration due to gravity which is equal to mass as shown below.
The deadweight of the train along the slope will bring the train downwards due to gravity. Hence the tractive effort required to overcome gravity on a gradient is given by,
Fg = 1000 × M × 9.81 × sinθ Newtons ...(1)
From the above figure, the gradient is expressed as rise in meters in a track distance of 100m and is denoted as a percentage gradient (G).
G = 100 × sinθ or sinθ = G/100
Substituting sinθ value in equation 1 we get tractive effort required to overcome gravity on a gradient as,
Fg = 1000 × M × 9.81 × (G/100)
Fg = 98.1 × M × G Newtons
Tractive Effort Required to Overcome Train Resistance :
The forces which resist the motion of the train are known as train resistances. They are of two types, one is mechanical resistance and the other is wind resistance. Again the mechanical resistance is of two types, one is internal friction which is between journals, axles, etc, and the other is external friction which is between track and wheels.
The wind is the other force that acts as train resistance and varies directly with the square of the speed. The train resistance is mathematically given as,
In the above equation, the first two terms represent mechanical resistance and the third quantity represents wind resistance. If 'r' is the specific resistance of the train per unit mass, then the tractive effort required to overcome the train resistance is given as,
Therefore, from the above three tractive effort equations, the total tractive effort required to propel the train is given as,
Ft = Fa ± Fg + Fr
Ft = 277.8 × Me × α ± 98.1 × M × G + M × r Newtons
Mechanics of Train Movement :
In the above-disccused equation, we have seen tractive effort required for propulsion of train. But the tractive effort transferred to the train driving wheel from the motor can be found from the mechanics of train movement.
The diving parts of an electric locomotive consist of a pinion and gear connection between the motor armature and wheel of the locomotive. The torque generated by the motor is transmitted to the wheel of the locomotive through the pinion and gear wheel as shown in the below figure.
The torque exerted by the motor is given as,
T = force × distance = F1 × (d1/2)
F1 = 2T/d1
The tractive effort transferred to the driving wheel from the motor is given as,
Where,- F2 = Tractive effort at driving wheel,
- F1 = Tractive effort at pinion,
- T = Torque developed by motor,
- D = Diameter of driving wheel,
- d = Diameter of the gear wheel,
- d1 = Diameter of pinion,
- η = Transmission efficiency,
- γ = Gear ratio = d/d1.
