Electrical Resistance is the important electrical quantity that determines the amount of current flowing through a material. Electrical Resistance, the name itself tells that it is a resistance or opposition to the flow of electric current in a material.
Every material possesses a finite amount of electrical resistance. Based on the amount of resistance the materials are categorized into conductors (which allow electric current freely), insulators (which do not allow electric current), and semiconductors (neither completely allow nor oppose electric current).
The resistance of a material depends upon its structure, nature, and also on its temperature. The change in temperature causes the atoms and electrons in the material to move around more, due to which the flow of electric current in the material gets affected.
The relationship between temperature and resistance is often described by a physical law called the Temperature Coefficient of Resistance. In this article let us learn about what is the temperature coefficient of resistance with its definition, formula, and numerical problems.
What is the Temperature Coefficient of Resistance?
The temperature coefficient of resistance is defined as the change in electrical resistance of a material per degree of temperature change. It shows the relation between variation in the resistance of a material with a change in its temperature.
Using the temperature coefficient of resistance we can define the value of change in resistance of a material as the temperature changes. The temperature coefficient of resistance is denoted by the Greek letter alpha (α).
Temperature Coefficient of Resistance :
Consider a material having resistance R0 at 0°C and Rt at t°C. It can be seen that the increase in resistance (Rt - R0) is,
- Directly proportional to the initial resistance i.e., (Rt - R0) ∝ R0 ...(1).
- Directly proportional to the rise in temperature i.e., (Rt - R0) ∝ t ...(2).
- Depends upon the nature of the material.
Combining equations 1 and 2, we get,
In the above equation, α0 is the constant called the temperature coefficient of temperature at 0°C. The value of α0 depends upon the nature of the material and temperature. Rearranging equation 3, we get,
Hence from equation 4, the temperature coefficient of resistance of a material is defined as the change in resistance per ohm original resistance per °C rise in temperature.
Substituting all the quantities in equation 4, we get,
Hence, the unit of temperature coefficient of resistance is per degree Celsius (/°C). Different materials have different temperature coefficients of resistance at 0 °C, due to which change in resistance is different for different materials even for the same change in the temperature.
Types of Temperature Coefficient of Resistance:
There are two types of temperature coefficient of resistance, they are positive and negative temperature coefficient of resistance.
Positive Temperature Coefficient of Resistance :
A positive temperature coefficient (PTC) means the effect of temperature on the resistance of a material is directly proportional to each other. In other words, if the resistance of a material increases with an increase in temperature, then it is said to have a positive temperature coefficient of resistance.
Electrical conductors such as gold, aluminum, silver, copper, mercury, etc., have a positive temperature coefficient of resistance. The availability of a large number of free electrons, makes conductors allow the flow of electric current through them easily.
When the temperature of a conductor material raises, the thermal energy creates vibrations in atoms. Due to this, the moving electrons in the material collide with other electrons slowing down their movement which results in cause of electrical resistance. The process of electron collision increases as the temperature of the conductor increases thereby increasing the resistance as represented in the below graph.
Therefore, the resistance of conductors will increase with the rise in temperature which is said to be known as Positive Temperature Coefficient of Resistance.
Negative Temperature Coefficient of Resistance :
A negative temperature coefficient (NTC) means the effect of temperature on the resistance of a material is inversely proportional to each other. In other words, the resistance of materials with a negative temperature coefficient decreases with an increase in temperature.
Materials like insulators and semiconductors have a negative temperature coefficient of resistance. Unlike conductors whose resistance increases with an increase in temperature, the situation is different in the case of insulators and semiconductors.
In insulators, the atoms have tightly bound electrons that cannot move freely throughout the material. Thus insulators have high resistance at normal conditions due to the availability of very few free electrons in their atoms. When the temperature of insulator material is increased, the atoms vibrate violently similar to conductors.
When there is a sufficient increase in the temperature of the insulator, the vibrations reduce the bond strength between electron and nucleus, resulting in the creation of free electrons which become charge carriers. Thus, an increase in the temperature of insulators decreases their resistance as shown in the below graph.
Therefore, when the temperature of insulators increases they behave as conductors. A similar process happens when the temperature of semiconductors rises thereby exhibiting a negative temperature coefficient of resistance.
Graphical Determination of Temperature Coefficient of Resistance :
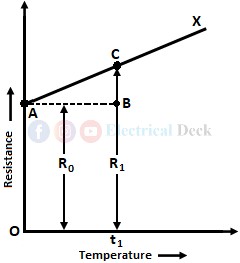
We can also obtain the value of the temperature coefficient of resistance of a material from a temperature-resistance graph of the material. The below shows the curve between resistance and temperature for a conductor.
We know that conductors have positive temperature coefficient of resistance which is shown by the straight line AX. It can be seen that, at 0°C temperature, the material's resistance is R0 represented by OA. When the temperature increases to t1°C, the resistance becomes R1.
From the definition of the temperature coefficient of resistance, we can write,
From the above graph, R1 - R0 = BC, and rise in temperature = AB. Therefore, the temperature coefficient of resistance at 0°C is simplified as,
In the above graph, BC/AB is the slope of the temperature-resistance graph. Therefore,
The above equation gives the temperature coefficient of resistance of a conductor at 0°C. The value of 'α' depends upon temperature. The value of α0 is maximum and it decreases with a rise in temperature.
Relation between Temperature and Resistance :
In the above temperature-resistance graph, we know that R0 and R1 are resistances of material at temperature 0°C and t1°C respectively. let α0 and α1 be the temperature coeffcient of resistance at 0°C and t1°C respectively. From the equation 5, we can write,
Similarly,
Since the slope of the temperature-resistance graph is constant,
The above equation gives the relation between α0 and α1. Similarly, we can get the value of 'α' at any temperature if the value of 'α' at 0°C is known.
Using the temperature coefficient of resistance we can determine the value of resistance at any temperature. If R1 and R2 are resistances of material at t1°C and t2°C respectively. If α1 is the temperature coefficient of resistance at t1°C. The relation between temperature and resistance is given as,
From the above equation, the change in resistance of material due to temperature depends upon,- The initial resistance of the material.
- The temperature coefficient of resistance 'α'.
- The amount of rise in temperature.
Temperature Coefficient of Resistance of Some Materials :
| Material | Temperature Coefficient of Resistance at 20°C (in /°C) |
| Aluminium | 0.00429 |
| Brass | 0.0015 |
| Copper | 0.00386 |
| Gold | 0.0034 |
| Iron | 0.00651 |
| Mercury | 0.0009 |
| Nickel | 0.00641 |
| Platinum | 0.003927 |
| Silicon | – 0.07 |
| Tungsten | 0.0045 |
Numerical Example :
A copper wire has a resistance of 0.85 ohm at 20°C and a temperature coefficient of resistance of 0.004°C at 0°C. What will be the resistance of copper wire at 40°C?
Given, α0 = 0.004°C, t1 = 20°C, t2 = 40°C, R20° = 0.85 ohm. We know that,
Therefore, the resistance of the copper wire at 40°C is given as,
Conclusion :
From this article, we can conclude that temperature affects the value of resistance of a material. The variation in resistance of a material with temperature is described as the temperature coefficient of resistance of that material. Generally, conductors have a positive temperature coefficient of resistance, whereas insulators and semiconductors have a negative temperature coefficient of resistance.