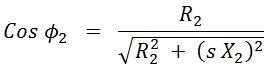The torque T, of an induction motor, is proportional to the product of stator flux per pole (Φ), rotor current (I), and the power factor of the rotor. The torque of an induction motor is due to the interaction of the rotor and stator fields and is dependent on the strength of the fields and their phase relationship.
Thus,T ∝ I2Cos Φ2Since rotor induced EMF/phase, E is proportional to the stator flux Φ.
i.e., E2 ∝ Φ
Therefore,
T ∝ E2 I2 Cos Φ2
But rotor current/phase,
and, Rotor Power factor,
Therefore,
Where, K = Constant of proportionality = 3*60/2π Ns
Another Method :
Let, T = Torque developed by an induction motor. We know that the Rotor input,
P2 = 2π Ns T/60
Therefore Torque,
Now, rotor input,
But rotor current/phase,
Therefore, rotor input,
Substituting the expression of P2 in equation (1), we get the equation of torque as,
Where, K = Constant = 3*60/2π Ns.
The above equation is the torque equation for an induction motor under the running condition. So torque developed at any load condition can be obtained, by knowing the slip of the induction motor at that load condition.
Starting Torque :
The torque produced by the motor at the start is called starting torque, Tst. At start, N = 0 and hence slip, s = 1. Therefore, starting torque can be obtained by substituting s = 1 in equation (2), i.e., torque equation under the running condition.
Comparison of Torques :
The performance of the motor is sometimes expressed in terms of comparison of various torques such as full-load torque, starting torque, and maximum torque.
Relation Between Full-load and Maximum Torque :
Let
sf = full-load slip
The expressions for full-load torque TFL, and maximum torque, Tmax is,
The ratio of full-load torque to maximum torque is,
Dividing numerator & denominator by X22, we get,
Relation Between Starting Torque and Maximum Torque :
The expression for starting torque Tst, and maximum torque, Tmax are,
By dividing the numerator and denominator by X22, we get
