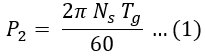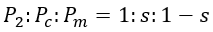Efficiency and Power Flow Diagram of Induction Motor

Power Transfer Stages of Induction Motor :

An induction motor converts electrical power supplied to it into mechanical power. The various stages in this conversion are called power transfer stages in an induction motor. The 3-phase power input to an induction motor i.e, stator input is,

P_in = √3 V_L I_L Cos Φ

Where V_L and I_L are the line values of stator supply voltage and current and Cos Φ is the power factor of the motor. A part of this power is consumed in stator iron and copper losses. The remaining power is transferred inductively to the rotor through the air gap. This is called rotor input P₂. Therefore,

P₂ = P_in - stator iron and copper losses

The rotor losses consist of the majority of copper loss and very small rotor iron loss which are generally neglected. By subtracting the rotor copper losses from P₂, we get the gross mechanical power developed by the motor P_m.

P_m = P₂ - rotor copper losses

A part of P_m is consumed as mechanical losses and the remaining is the power available to the load at the shaft. This is called as Net Output Power of the Motor P_out. The above stages can be shown diagrammatically called as Power Flow Diagram of Induction Motor.

Relation Between Rotor Input, Rotor Copper Losses, and Rotor Output :

Let,

• P₂ = Rotor input
• P_c = Rotor copper losses
• P_m = Gross mechanical power developed or rotor output
• T_g = Gross torque developed by the rotor in N-m.

The actual torque available at the shaft is called Shaft Torque or Useful torque T_sh,

• T_sh = Gross torque
• T_g = Torque lost due to the friction and windage losses.

Now input to the rotor is through the air gap with the help of a rotating magnetic field which is rotating at a speed of N_s rpm. The rotor input can be expressed in terms of gross torque T_g and speed as,

Now torque developed remains the same, but the rotor output which is gross mechanical power developed P_m is at a speed 'N' rpm. So from the output side, we can write,

We know that, rotor copper losses,

Dividing equation 3 by 1, we get,

So rotor copper losses are slip times the rotor input. Now gross mechanical power developed,

So gross mechanical power developed is (1 - s) times the rotor input. Dividing equation 4 by 5, we get,

From the above, it can be concluded that,

Gross Torque and Shaft Torque :

The torque produced by the rotor is gross mechanical torque and due to mechanical losses entire cannot be available to drive the load. The load torque is net output torque called shaft torque or useful torque. Therefore, shaft torque is given as,

Gross Torque is given as,

where,

• T_lost = Torque lost due to mechanical losses
• P_out = Motor output
• P_m = Mechanical power developed
• N = Motor speed.

Efficiency of an Induction Motor :

The ratio of net power available at the shaft (P_out) and the net electrical power input (P_in) to the motor is called as overall Efficiency of an Induction Motor.

The maximum efficiency occurs when variable losses become equal to constant losses.

The normal efficiency curve of the motor is shown above. Therefore, rotor efficiency is given by,