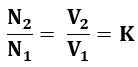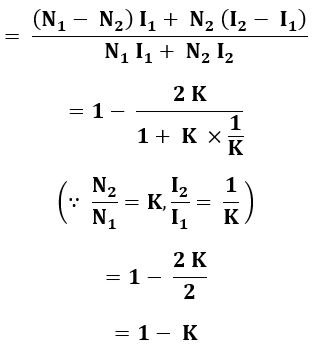What is an Autotransformer?

An autotransformer is a special type of transformer because its construction is different from a normal transformer. It is a transformer where the secondary winding is also part of the primary winding. i.e., It is a single winding transformer where the winding is common for both the primary and secondary sides.

Its operating principle and general construction are the same as that of a conventional two-winding transformer. Economically this type of transformer is very cheaper compared to a normal transformer. Let us see the construction and operation of the autotransformer.

Construction & Working of Autotransformer :

The construction and working principle of an autotransformer are similar to a normal two-winding transformer. But, here only one winding is wound with the laminated core as shown in the below figure. The secondary winding of the transformer is taken from the portion of the primary winding. The amount of the portion connected to the secondary winding depends upon the voltage rating.

By interchanging the winding connection (making secondary as primary and vice-versa) we can make an autotransformer either as a step-up autotransformer or step-down autotransformer.

For a step-down autotransformer (V₁ > V₂), the connection is made in such a way that the entire winding act as the primary winding, and the secondary winding will be part of the primary winding (but not equal to primary winding) i.e., N₁ > N₂.

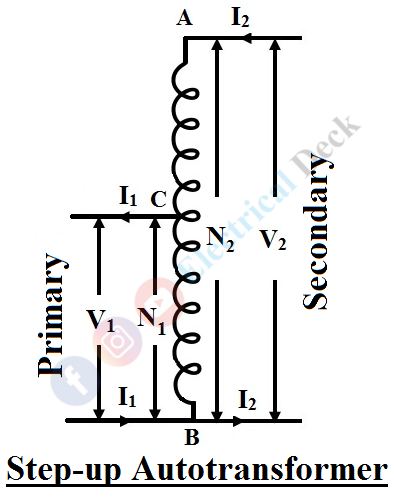
For a step-up autotransformer (V₁ < V₂), here the whole winding will be made as to the secondary side and the primary side will be part of the secondary side (but not equal to the secondary side) as shown below, i.e., N₁ < N₂.

The main use of autotransformer is due to its reduced size by making a single winding as the primary and secondary side. Which in turn reduces the amount of copper used.

Copper Saving in Autotransformer :

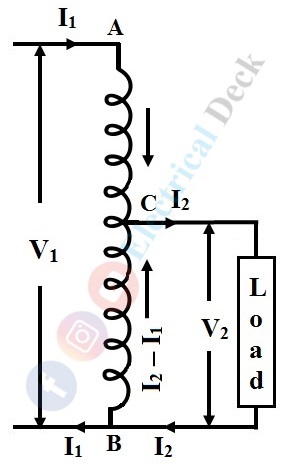
Let us consider AB as a primary winding having N₁ turns and BC as a secondary winding having N₂ turns as shown in the above figure. Then the transformation ratio K, of the transformer will be,

Now, by neglecting iron losses and no-load current. The current in section CB is a vector difference between I₂ and I₁. But in practice, the two currents I₂ will be in phase opposition. Therefore, the resultant is (I₂ - I₁) where I₂ is greater than I₁.

In a transformer, the weight of the copper conductor used will depend upon its cross-section area and the total length of the conductor. Therefore, as the length of the conductor (winding) increases the number of turns around the core increases, and as the cross-section of the conductor increases the current carrying capacity of the conductor increases. Hence the weight of the conductor is proportional to the product of current and the number of turns in a transformer.

Weight of copper used in autotransformer :

Weight of copper in section AC ∝ (N₁ - N₂) I₁.
Weight of copper in section BC ∝ N₂ (I₂ - I₁).
Total weight of copper in autotransformer = (N₁ - N₂) I₁ + N₂ (I₂ - I₁).

Weight of copper used in two-winding transformer :

Weight of copper required for primary ∝ N₁ I₁.
Weight of copper required for primary ∝ N₂ I₂.
Total weight of copper in two-winding transformer = N₁ I₁ + N₂ I₂.
Thus,

= Weight of copper required for autotransformer / Weight of copper required for two-winding transformer

The weight of copper in autotransformer W_a is equal to (1 - K) × Weight of copper in two-winding transformer W_o. Therefore, the weight of copper savings is,
W_o - W_a
= W_o - (1 - K) W_a
= W_o K
= K × Weight of copper in a two-winding transformer.
Hence, the saving will increase as the difference between K and unity will decrease.
It can be proved that power transformed is = (1 - K) input.
The rest of the power is conducted directly from the source to the load.

Advantages of Autotransformer :

Continuously varying voltage can be obtained.
Autotransformer requires less copper than a two-winding transformer of a similar rating.
Autotransformer is cheap.

Disadvantages of Autotransformer :

Autotransformer application is limited, as it can be used where K (transformation ratio) differs little from unit only.

Applications of Autotransformer :

Due to its voltage varying feature by reducing the per phase supply voltage we can use an autotransformer for starting induction motors and synchronous motors. Autotransformers used for this purpose are also known as auto-starters.
Autotransformers are used as boosters to raise the voltage in ac distribution cables.
A continuously variable autotransformer finds useful applications in the electrical testing laboratory.
An autotransformer is also used as the furnace transformer where there is a need for regulation of voltage in power supply at our place.

What is an Autotransformer? - Construction, Working & Applications