A Transformer is a static device that works on the principle of Magnetic Induction. When an alternating supply is given to its primary winding a magnetizing current will circulate through the primary winding and set up a magnetic flux. This magnetic flux circulates through the low reluctance path provided in the transformer (i.e., the core of the transformer) and links with the secondary winding.
As the supply given is alternating the nature of the flux produced will also be alternating. This alternating flux when links with the secondary winding, it induces an electro-motive force (emf) in the secondary winding according to faraday's law of electromagnetic induction, and there will be a circulation of currents in the secondary winding. The amount of emf induced will depend upon the number of turns in the primary and secondary winding.
EMF Equation of Transformer :
The EMF equation of a transformer gives the amount of emf induced in the primary and as well as in secondary windings. Consider a transformer of N1 turns in the primary winding and N2 turns in the secondary winding. When voltage V, is applied to the transformer, emf E1 induced in the primary winding will induce another emf E2 in the secondary winding by mutual induction as shown below.
The frequency of the induced emf will equal the supply frequency f, and the magnitude of both fluxes due to magnetizing current Im will be the same as supply magnitude, i.e., sinusoidal in nature.
Let,- Φ = Maximum flux in core in weber = Maximum flux density Bm x area A
- N1 = Number of primary turns
- N2 = Number of secondary turns
- f = supply frequency in Hz
- E1 = RMS value of primary induced emf
- E2 = RMS value of secondary induced emf.
As the input given to the transformer will be a sinusoidal waveform. We can see that the time taken to increase the flux from zero to maximum value Φm, in terms of frequency is given as 1/4f second, i.e., in a sinusoidal waveform, the maximum current which gives the maximum flux will be at 1/4f as shown in the below.
We know that from Faraday's Laws of Electro-Magnetic Induction, the emf induced is directly proportional to the rate of change of flux. The average rate of change of flux will be, As the emf induced will be equal to the rate of change of flux, the average e.m.f induced per turn will be, Since the flux Φ varies sinusoidally, we know the form factor of a sinusoidal waveform is 1.11 (Form factor = RMS value / average value). Therefore, the RMS value of the induced emf per turn will be, The resultant RMS value of the induced emf we derived will be in terms of the per-turn of the winding. But there are N1 and N2 number of turns in the primary and secondary windings. Therefore, the total RMS value of emf E1 and E2 induced in the primary and secondary winding is given as,
Turn & Transformation Ratio of Transformer :
Turn Ratio of Transformer :
From the emf equation of the transformer, if E1 and E2 are the emf induced in the primary and secondary winding. Then the ratio of their turns N1 and N2 in the primary and secondary winding is given as,
The transformation ratio K of a transformer is defined as the ratio of their secondary induced emf to the primary induced emf.
- If V2 > V1 or N2 > N1 i.e., K > 1 then the transformer will work as a step-up transformer.
- If V1 > V2 or N1 > N2 i.e., K < 1 then the transformer will work as a step-down transformer.
Current Ratio :
Consider an ideal transformer whose losses are negligible and zero. For an ideal transformer, the input power will equal the output power (i.e., input VA = output VA).
Hence, in a transformation ratio K, primary and secondary currents are inversely proportional to their respective turns.




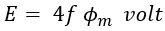






Oh wow, I got through several websites like www.eengineer.in, byjus and other tutorial website but never had a chance to get this type of explanation to the knowledge great work.
ReplyDelete