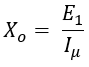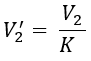Equivalent Circuit of Transformer Referred to Primary & Secondary

Basically, an equivalent circuit is representing all the parameters of the transformer in a form of a circuit or diagrammatical manner. The equivalent circuit of the transformer can be used to understand the behavior of the transformer under various conditions.

Calculation of various parameters of the transformer like resistance, reactance, and impedance on the primary and secondary side can be done easily which in turn also used for determining the regulation, efficiency, and losses of the transformer.

Equivalent Circuit of a Transformer :

Consider a transformer with V₁ and I₂ are the primary voltage and current. Similarly, V₁ and I₂ are the secondary voltage and current. Let, E₁ and E₂ are the EMFs induced in primary and secondary windings respectively as shown below.

For the above transformer, the equivalent circuit with having transformation ratio K is shown below.

In the above circuit diagram, the primary current of the transformer serves two components I_o and I₂. The no-load current I_o, also known as the magnetizing current also produces flux and magnetizes the core with losses in the core.

• The core losses (hysteresis loss and eddy-current loss) are represented by a non-inductive resistance R_o taking working component I_w. The current I_w, component current of I_o flow through the resistance R_o such that,
  
• The emf E₁ is induced in the primary winding due to flux produced by the magnetizing current I_μ. The magnitude of emf E₁ will be less and in opposition to the applied voltage V₁. The reactance X_o due to flux Φ, which is connected in parallel to the resistance R_o is such that,
  

Here, R₁ X₁ and R₂ X₂ are the drops due to primary and secondary winding resistance and leakage reactance respectively. The current I₂ is the counter-balance current I₂ of secondary on the primary. Now, we can further simplify the equivalent circuit either by shifting the primary parameters to the secondary side or vice-versa, this reduces the complexity of the circuit and computation. This can be done by using the transformation ratio of the transformer.

Equivalent Circuit of Transformer Referred to Primary Side :

The above equivalent circuit of the transformer can be modified by transferring the voltage, current, and impedance of the secondary side to the primary side as shown below figure.

By transferring all the parameters of the secondary side to the primary side with transformation ratio K. Then,

• The primary equivalent of the secondary emf,
  
• The primary equivalent of secondary terminal voltage,
  
• The primary equivalent of the secondary current,
  
• Similarly, the secondary resistance, reactance, and impedance referred to as primary is given as,
  

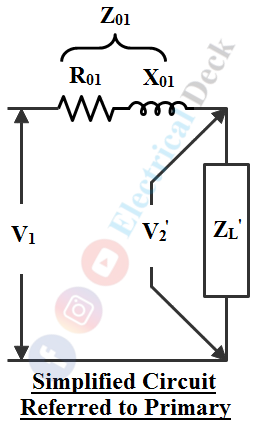
The equivalent circuit can further be modified by transferring R_o and X_o (exciting circuit) towards the left end known as the approximate equivalent circuit as shown in the figure below. The error introduced by doing so is small and can be neglected. It should be noted that in this case R_o = V₁/I_w and X_o = V_o/I_μ.

Since no-load current I_o is very small, the circuit can be further simplified by neglecting I_o taking as I₁' = I₁ shown in the below figure. Here, R₀₁ (R₁ + R₂') and X₀₁ (X₁ + X₂') are the total equivalent resistance and reactance of the transformer referred to as primary.

Equivalent Circuit of Transformer Referred to Secondary Side :

Similarly, how the transformer equivalent circuit is referred to the primary side, we can also refer primary side parameters towards the secondary side by transferring the primary side to the secondary side as shown below.

By transferring all the parameters of the primary side to the secondary side with transformation ratio K. Then,

• The secondary equivalent of the primary emf,
  
• The secondary equivalent of primary voltage,
  
• The secondary equivalent of the primary current,
  
• Similarly, the primary resistance, reactance, and impedance referred to as secondary is given as,
  

Similarly, by neglecting the no-load current I_o the simplified equivalent circuit referred to secondary side is shown below. Here, R₀₂ (R₁' + R₂) and X₀₂ (X₁' + X₂) are the total equivalent resistance and reactance of the transformer referred to as secondary.

From the above, we can conclude that,

• If the equivalent circuit parameters are referred to as the primary. The secondary parameters must be divided with the transformation ratio K except for the secondary current where it is multiplied.
• If the equivalent circuit parameters are referred to the secondary. The primary parameters must be multiplied with the transformation ratio K except for the primary current where it is divided.