An ideal transformer, according to our assumptions, has got zero losses with no resistance in its primary and secondary windings. But in practice, it is impossible to build such a transformer.
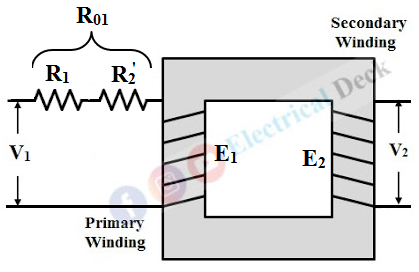
In the actual transformer, both primary and secondary windings have got some resistance internally due to the property of the conducting material used. This resistance causes some voltage drop as well as power loss in their respective windings. The figure below shows the internal resistance of the primary and secondary windings connected externally.
It is essential to calculate the effective resistance of the transformer in order to determine losses and efficiency. To reduce the complexity of calculation for finding the total resistance of the transformer (i.e., both primary and secondary winding resistance) the total resistance will be referred to any one side of the transformer i.e., either primary or secondary. It also helps in making the equivalent circuit of the transformer referred to as the primary or secondary side.
Let,- R1 & R2 = Primary and secondary winding resistance
- E1 & E2 = Primary and secondary induced emf
- V1 & V2 = Primary and secondary voltages
- I1 & I2 = Primary and secondary currents.
Now, the voltage across the primary and secondary winding is given by,E1 = V1 - I1 R1V2 = E2 - I2 R2Here, I1 R1 and I2 R2 are the primary and secondary voltage drops respectively as shown in the below phasor diagram.
Equivalent Resistance of Transformer :
The primary resistance R1 and secondary resistance R2 are the resistance of the transformer primary and secondary windings. Which can be transferred from one side to the other and vice-versa. The advantage of transferring the whole resistances to one side is for simplicity of calculations. The resistance from one side to another side can be transferred on an equal power loss basis.
Equivalent Resistance Referred to Primary Side :
The copper loss in secondary is I22 R2. If R2' is the equivalent resistance referred to primary would have caused a power loss (copper loss) I12 R2'. Then,
As the no-load Io is small, if we neglect it. Then, the secondary resistance referred to primary would be,
Therefore, the total or effective, or equivalent resistance R01 referred to the primary side is given by,
Equivalent Resistance Referred to Secondary Side :
Similarly, if primary resistance R1 is transferred to the secondary side and is represented as R1'. Then the power loss (copper loss) of the primary winding referred to secondary side would be I22 R1'.
Therefore, the total or effective or equivalent resistance R02 referred to secondary side is given by,
From the above two techniques, it can be noted that,- When primary resistance is shifted to secondary, multiply it by K2.
- When secondary resistance is shifted to the primary divide it by K2.
