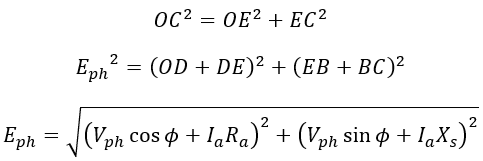Phasor Diagram of Synchronous Generator or Alternator

In the last article, we have derived the equation for EMF induced in the alternator. The equation for per-phase induced emf E_ph in an alternator is given as,

E_ph = 4 K_f K_c K_d f Φ T volt

When an alternator is loaded the whole induced emf doesn't appear across the output terminals. As the load on the alternator is varied, its terminal voltage V_ph also varies due to the following drops,

• Voltage drop I_aR_a due to armature resistance R_a.
• Voltage drop I_aX_s due to armature leakage reactance X_L.
• Voltage drop due to armature reaction.

The induced emf in the alternator has to supply the above drops while supplying the load. Therefore the equation for terminal voltage of an alternator is given as,

E_ph = V_ph + I_aR_a + I_aX_s volt

From the above voltage equation, let us draw the phasor diagram of a synchronous generator operating at different load power factors. The relation between terminal voltage and current for power factor analysis can be done by the phasor diagram.

Let,

• E_ph = Induced emf on load per phase.
• V_ph = Terminal voltage per phase
• I_a = Armature current
• Φ = Phase angle between I_a and V_ph (i.e., p.f.)
• R_a = Armature resistance per phase
• X_s = Synchronous reactance (leakage reactance + armature reaction reactance)

Taking V_ph as the refernce phasor. The phase relationship between armature induced emf E due to field flux Φ_f and the current flowing through the armature I_a depends upon the power factor of the load.

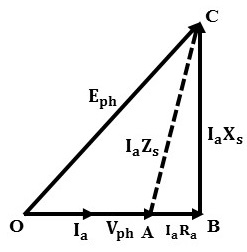
Phasor Diagram at Unity Power Factor Load :

When the alternator is driving a unity power factor load (resistive) i.e., cos Φ = 1. The armature current I_a will be in phase with V_ph as shown below.

From the triangle OBC, the expression for induced emf E_ph is given as,

At unity power factor cos Φ = 1 and sin Φ = 0. The equation is modified as,

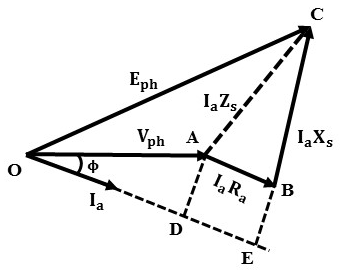
Phasor Diagram at Lagging Power Factor Load :

For lagging power factor loads the current I_a will lag the terminal voltage V_ph with an angle Φ. At zero lagging power factor (pure inductive) the current I_a lags the voltage V_ph exactly by 90°. The below shows the phasor diagram for the lagging power factor.

The armature resistance drop I_aR_a is due to armature current I_a. Hence it always lies in phase with current I_a i.e., DE. Therefore, from the triangle OCE,

Phasor Diagram at Leading Power Factor Load :

Similar to the lagging power factor the current I_a leads the voltage V_ph by Φ at leading power factor loads as shown below. At zero leading power factor (pure capacitive) current I_a lead V_ph exactly by 90°.

From triangle OCE,

From the above, we can conclude that,

• For unity and lagging p.f. the sign of I_aX_s will be positive. Because the armature reaction effect in X_s will be demagnetizing and cross-magnetizing effect at unity and lagging power factor.
• For leading p.f. the sign of I_aX_s will be negative. Thus V_ph is more than E_ph due to the magnetizing effect of armature reaction.