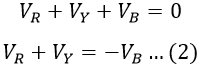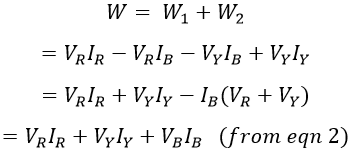The disadvantage of the one wattmeter method is that it cannot be used for three-phase systems that carry unbalanced loads. Also, in three wattmeter method for star-connected load, it is difficult to get a neutral point to connect voltage coils, and the current coils are inserted in a closed delta for delta connected load. These drawbacks can be overcome by the Two Wattmeter method. The two wattmeter method of three-phase power measurement is given from Blondel’s theorem.
Blondel’s Theorem for 3-Phase Power Measurement :
Blondel's theorem tells about the number of wattmeters required to measure three-phase power.
It states that, in order to measure power in a network with n number of lines. The total number of wattmeters required is equal to n, and total power is the sum of all the wattmeters readings.
It is in such condition that, if current coils of each wattmeter are connected in each line and corresponding voltage coils are connected such that, one end to their respective line and other ends of all the voltage coils are connected together forming a common point.
Suppose, if the common point is to be taken on any one of the lines. Then the other end of the voltage coils is connected to that common line (i.e., common point). In such conditions, the power can be measured by (n-1) wattmeters. Thus for measuring 3-phase power, only 2 wattmeters are required, this is called Two Wattmeter Method.
Measurement of Power by Two Wattmeter Method :
This method is employed for the power measurement of a 3-phase 3-wire unbalanced or balanced system. The current coils are connected in series with the two lines. One end of each voltage coil is connected to the line in which current coils are placed and the other ends of two voltage coils are brought out and are connected to the third line.
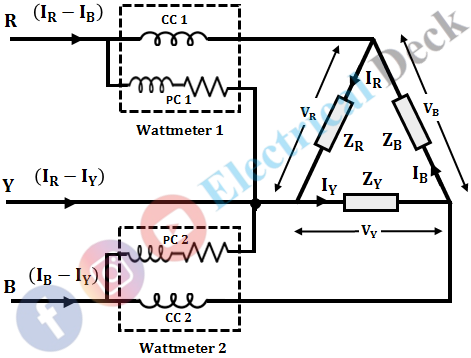
The connection diagram for the two wattmeter method of measuring the three-phase power of star and delta connected loads is shown below.
Measurement of Power by Two Wattmeter Method in Star Connection :
Let the phase voltages and line currents of the phases R, Y, and B be (VR & IR), (VY & IY), and (VB & IB). Let W1 and W2 be the power measured by wattmeters 1 and 2 respectively.
From the above figure, the power measurement by wattmeter 1 is,W1 = (VR - VY) IR = VR IR - VY IR
Power measurement by wattmeter 2 is,W2 = (VB - VY) IB = VB IB - VY IB
At neutral point N, we have,
Therefore, total power i.e., sum of both the wattmeter readings is,
Hence, the sum of both the wattmeter readings gives the total power consumed by the load.
Measurement of Power by Two Wattmeter Method in Delta Connection :
Let the phase voltages and line currents of the phases R, Y, and B be (VR & IR), (VY & IY), and (VB & IB). Let W1 and W2 be the power measured by wattmeters 1 and 2 respectively.
From the above figure, the power measurement by wattmeter 1 is,W1 = VR (IR - IB) = VR IR - VR IB
Power measurement by wattmeter 2 is,W2 = -VY (IB - IY) = -VY IB - VY IY
Here, VY is taken as negative because it is being measured from phase B to Y while VY is from Y to B. Applying KVL to the delta connected load, we get,
Therefore, total power i.e., sum of both the wattmeter readings is,
In this case also, the sum of both the wattmeter readings gives the total power consumed by the load. Hence, at any instant regardless of the power factor, the sum of two wattmeter readings gives total instantaneous power in a three-phase unbalanced load.
