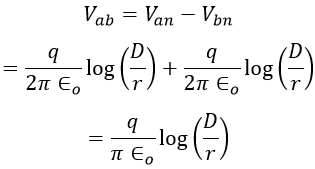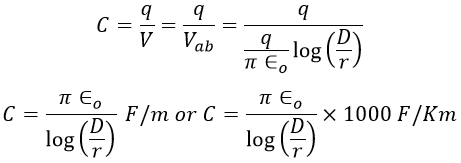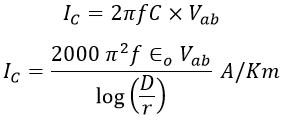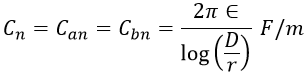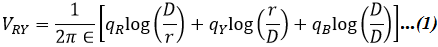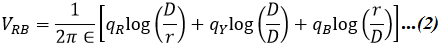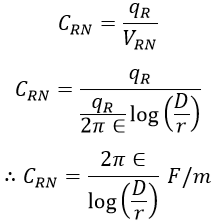We know that a capacitor is formed when two conducting plates are separated by an insulating medium. Similarly, due to potential difference, there exists a capacitance between two conductors of transmission lines in which air between them act as the insulating medium.
Due to this presents of capacitance, there exists a charging current even when the line is open-circuited, similar to the charging of plates of the capacitor. Hence, it is important to take into account the capacitance of the transmission line.
The capacitance between two conductors of the transmission line is the electric charge per unit potential difference between two conductors. It is uniformly distributed throughout the two parallel conductors and its value depends upon the size, shape, and distance between the conductors.
For transmission lines of short distance (below 80Km), the effect of capacitance is negligible and can be neglected. But for long transmission lines with higher operating voltages, there will be the effect of capacitance on the transmission lines i.e., its effect on power loss and voltage regulation of the system. Hence, it is predominant to consider capacitance in analysis in case of long transmission lines.
Capacitance of Two-Wire Transmission Line :
Consider a single-phase line consisting of two solid round conductors a and b of radius r meters and spaced at D meters as shown in the figure below.
Let us assume that r << D. So the charge density will be uniform throughout the length of the conductors as the charge on one conductor does not affect the charge on the other. Let a charge Q coulombs exist on conductor a. Since it is a single-phase line, the other conductor acts as a return conductor, so the charge on conductor b will be -q coulombs.
Now, the potential difference between conductor a and neutral point n at infinity is,
Similarly, the potential difference between conductor b and neutral point n is,
Therefore, the potential difference between conductors a and b is,
The capacitance between two transmission lines is the charge on the conductors per unit of potential difference between them i.e.,
The above equation gives the line-to-line capacitance i.e., the capacitance between two conductors. The charging current of the line per km is,
For the purpose of transmission line modeling, it is important to find line-to-neutral capacitance i.e., the capacitance between a conductor and neutral. The below shows the idea of line-to-neutral capacitance by considering the potential difference between the two lines is zero such that the neutral point n is at the ground potential.
From the above, the line-to-neutral capacitance or capacitance to ground is given as,
Capacitance of Three Phase Transmission Line With Symmetrical Spacing :
Consider a 3-phase overhead transmission line consisting of the conductors R, Y, and B with radii r spaced symmetrically, such that the distance between any two conductors is d as shown below.
Further, assume that qR, qY, and qB be the charges uniformly distributed on the conductors R, Y, and B respectively such that qR + qY + qB = 0. The voltage drop between the conductors R and Y is given by the sum of the voltage drops due to all the three conductors i.e.,
Similarly, the voltage drop between the conductors R and B is given by,
Phasor diagram of the voltage VRY, VYB, and VBR is shown below,
From the phasor diagram we have,VRY + VRB = 3 VRN ...(3)Now, adding equations 1 and 2, we get,
Therefore, the line to neutral capacitance is given by,
It can be seen that the line-to-neutral capacitance of the symmetrically spaced three-phase transmission line is same as that of the two-wire transmission line.
