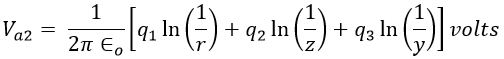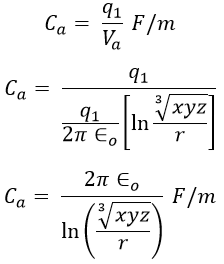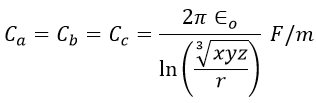Capacitance of Three Phase Transmission Line with Unsymmetrical Spacing :
Consider a three-phase overhead transmission line with unsymmetrical spacing between the conductors a, b, and c as shown in the figure below.
Let the voltages Va, Vb, and Vc are supplied to the conductors a, b, and c resulting in the charges q1, q2, and q3 such that, q1 + q2 + q3 = 0 (assuming balanced condition). Let x, y, and z be the spacing between the conductor a, b, and c respectively and r be the radius of each conductor.
Since the conductors are spaced unsymmetrically, the value of voltage from conductor to neutral is not the same for the three conductors. In order to make these voltages equal, the lines are transposed. After that, the value of any conductor to neutral becomes the same and it is given by the average values of the voltage in each position the conductor takes during transposition.
Now, concentrating on conductor 'a' and calculating the voltages in three positions, it takes during the transposition, which is shown below.
- When the conductor 'a' is in the position as shown in figure 1 above, the voltage is given by,
- When the conductor 'a' is in the position as shown in figure 2 above, the voltage is given by,
- When the conductor 'a' is in the position as shown in figure 3 above, the voltage is given by,
Therefore, the average value of the voltage of the conductor 'a' is given by,
At balanced condition q1 + q2 + q3 = 0. From this q2 + q3 = -q1. Now the above equation can be modified as,
We know that the capacitance of conductor 'a' is given by,
The above equation gives the capacitance of conductor 'a'. In a similar fashion, the capacitance of the conductors 'b' and 'c' can be formed. They are given by,
