There are two main laws of illumination of a surface, they are,- Inverse Square Law, and
- Lambert's Cosine Law.
Inverse Square Law :
The inverse square law states that the illumination on the surface is inversely proportional to the square of the distance between the surface and the light source.
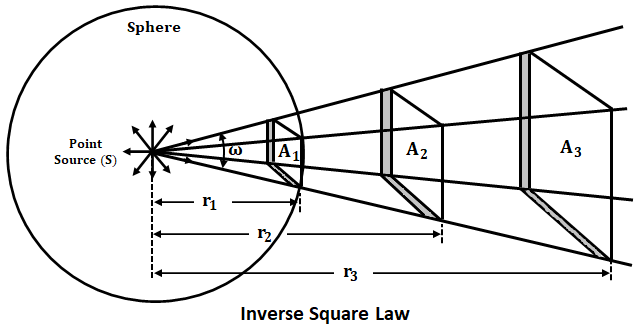
But the drawback of inverse square law is that this law is only applicable if the light source is considered as a point source. If a point source that emits an equal amount of light in all directions is placed at the center of the hollow sphere, then the light flux will reach all over the inner surface of the sphere uniformly i.e., an equal amount of light flux will be distributed over every square millimeter of the sphere.
Now if suppose the radius of the sphere is increased, the same amount of light flux from the point source will be distributed over the increased inner surface area proportional to the square of the radius i.e., every square millimeter of the sphere will diminish at the rate of increase in the sphere radius and will be inversely proportional to the square of the distance between source and surface.
Proof :
Let us prove the above discussed inverse square law mathematically. Consider two surface areas A1 and A2 placed at distances r1 and r2 respectively from the point light source (S) as shown below.
Let 'I' be the luminous intensity of the point source and the solid angle subtended at 'S' be ω steredains. Assuming that all the light flux is reaching the surface area. The total flux radiated in the direction of surfaces is given as,
In the above equation, ω is expressed as A/r2, where A is the area of the surface. From this the area of two surfaces A1 and A2 is given as,A1 = ω × r12 and A2 = ω × r22
Therefore, the illumination E1 on the surface area A1 is,
Similarly, the illumination E2 on the surface area A2 is,
For example, a light source 'S' gives an output of 'F' lumens within the solid angle 'W' enclosed by four lines OA, OB, OC, OD. The whole of the light will be falling on the surface 'A1', placed at the right angle to the axis of the beam and at a distance of 1m from the source, the illumination on the surface A1 is F/A1 lumen per m2.
If the distance of the surface is increased (considering the new surface as A2) from 1m to 2m from the same point source, the illumination on it will be decreased by 1/4 of that of A1. (A2 = 22 = 4 = 4A1 and since the total lumens will be the same as before, therefore, the illumination has to decrease 1/4 of that of A1).
Similarly, if the distance of the surface is increased to 3m away from the point source, the illumination will be decreased by 1/9 that of its original value. Hence it is proved that illumination on the surface is inversely proportional to the square of the distance between the surface and the light source.
Lambert's Cosine Law :
Lambert's cosine law states that the illumination (E) at any point on the surface is proportional to the cosine of angle which direction of the incident light flux makes with the normal (perpendicular) at that point.
The light flux received by the surface area changes with the change in angle between normal to the surface and the direction of the light flux. The illumination is maximum when the light flux falling is equal to normal to the surface, if the surface is inclined to the light flux falling, then the illumination is reduced.
Proof :
Let us prove the above discussed Lambert's cosine law mathematically. Consider a point source 'S' at a height 'h' from the surface CD. Assume that surface CD subtends solid angle 'ω' at point source 'S' as shown below. Let AB be the inclined surface area normal to the light flux with E as the center point of the surface.


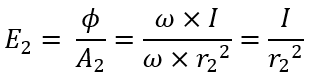

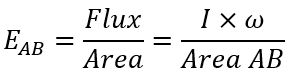

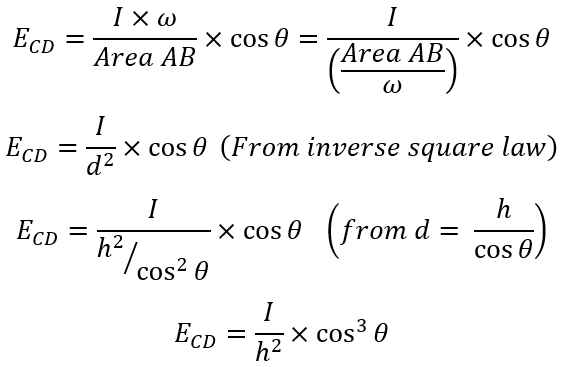
thank yuh
ReplyDelete