Generally, we assume the luminous intensity or the candle power emitted from the light source will be distributed uniformly in all directions. But in practice, most of the light sources (lamps) have a non-uniform distribution of luminous flux i.e., luminous intensity is not the same in all the directions. This non-uniform distribution of luminous flux is due to the unsymmetrical shape of the light source.
For designing any light installation, it is essential to know how exactly the light is distributed and this information is usually obtained by using an intensity distribution curve called Polar Curve. The polar curves represent the distribution of light or luminous intensity of a light source in all directions or over the surrounding surface.
The polar curves are drawn by taking luminous intensities in all the directions at an equal angular displacement. A radial ordinate from the light source in any direction represents the luminous intensity of the light source in that direction. The polar curves are of two types they are,
- If the luminous intensity is measured in a horizontal plane about a vertical axis and a curve is plotted between the candle power and the angular position, a curve known as Horizontal Polar Curve is obtained as shown below.
- If the luminous intensity is measured at the angular position in a vertical plane, a polar curve in the vertical plane called a Vertical Polar Curve is obtained as shown below.In the above polar curve, the depression of the curve at 180° is due to the lamp holder due to which there is less luminous intensity in that direction.
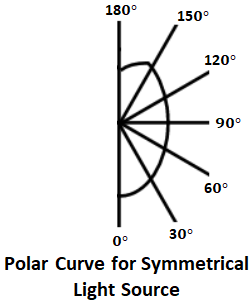
If the light source or attached reflector is of symmetrical type, then two halves of the polar curve will be similar and in such case, the polar curve can be represented by indicating only a half portion of it as shown below. But for luminous intensity from a light source of unsymmetrical shape, curves in a number of planes are drawn to represent the adequate distribution of luminous intensity.
By using polar curves mean horizontal candle power (MHCP) and mean spherical candle power (MSCP) can be determined. It is also used to determine actual illumination on a surface from vertical polar curves by calculating luminous intensity in that particular direction.
Measurement of MHCP and MSCP :
The Mean Horizontal Candle Power (MHCP) of a lamp can be determined from the horizontal polar curve by taking the mean value of the candle power in a horizontal direction, and the Mean Spherical Candle Power (MSCP) of a lamp can be found from the vertical polar curve by applying Rousseau's construction.
Consider a vertical polar curve consisting of two symmetrical lobes along YOY' axis. Then the Rousseau's curve can be constructed as follows,- Firstly a circle of any radius is drawn by taking the center (O) as the pole of the polar curve.
- Draw a line AB equal and parallel to the vertical diameter (YOY') of the circle.
- Now draw a line OCD such that C lies on the polar curve and D lies on the circle.
- Let E be the projection of line OCD onto the parallel line AB.
- From point E, erect an ordinate in such a way that EF = OC (radius of the polar curve).
- Similarly, from line AB, ordinates equal to the corresponding radius on the polar curve are erected such as IJ = OG, MN = OK, BR = OP, and so on.
The curve obtained by joining the ends of these ordinates is known as Rousseau's curve. Now the mean spherical candle power (MSCP) of the lamp is determined by calculating the mean ordinate of Rousseau's curve. The mean ordinate of the Rousseau's curve is,