Cross-field Theory of Single phase Induction Motor

It is interesting to know how a single-phase induction motor can able to rotate when an initial rotation or starting torque is given to it. This can understand with the help of cross-field theory and double-revolving field theory.

Motor at Standstill :

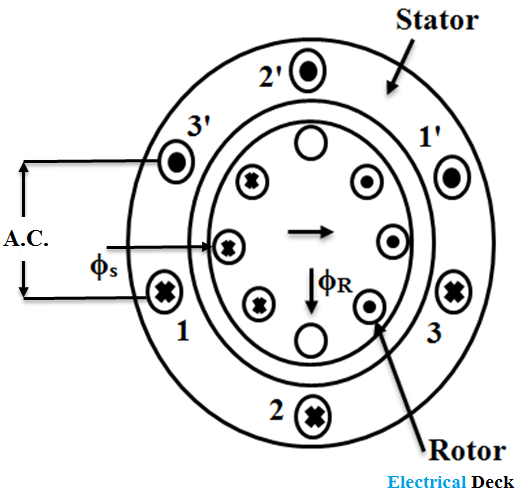
Consider standstill conditions with the stator winding connected to a single-phase AC supply. The stator current establishes a field that acts along the horizontal axis as shown in the below figure. The stator field is alternating in polarity and varies sinusoidally with time.

The alternating field will induce an emf in the rotor winding by transformer action. This emf will cause a current to flow in the rotor winding.

The directions of currents in the rotor conductors are also shown. The rotor currents establish poles on the rotor surface and these are in direct line (along the horizontal axis) with the stator poles. The axis of the stator and rotor fields are aligned.

The forces on the rotor conductors in the top half are in a downward direction, whereas the forces on the rotor conductors in the bottom half are in the upward direction. The two sets of forces will cancel and the rotor will experience no torque.

Motor at Running :

When, however, the rotor is made to rotate say in the clockwise direction by some external means, the rotor conductors cut across the stator field, causing an emf to be generated in them.

The direction of the emf is determined by fleming's right-hand rule, will be outward on one side of the vertical axis and inward on the other side of the vertical axis as indicated by the dots and crosses as shown in the below figure.

The generated rotor emf varies in phase with the stator current and flux. The rotor current due to these emf lags by nearly 90° owing to low 'R' and high 'X' of the rotor winding.

The field produced by the rotor currents is at right angles to the field by the stator currents hence it is known as a cross field. Thus the stator field Q_s and rotor field Q_r are in space and time quadrature.

These two fields will produce a resultant revolving field which will rotate in the direction in which the rotor was given an initial rotation. Hence torque is exerted on the rotor and the motor continues to rotate.

From the above discussion, it may be concluded that :

1. At standstill, there can be no cross field only the pulsating stator field and therefore the inherent starting torque of a single-phase induction motor is zero.
2. If, however, the rotor is made to run by some external means, then it will continue to develop torque in the direction of rotation.