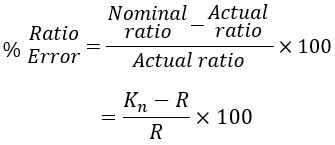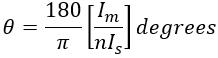In the last article, we have seen about the construction and working of a current transformer. A current transformer is a special-purpose transformer used to measure high currents in transmission and distribution systems. But for a current transformer, it is necessary to have exactly the same current ratio as that of the turns ratio. Also, the secondary current of the current transformer must be in phase opposition (180° phase displacement).
So that the calculated primary current from the measured secondary current will be accurate. But in a current transformer, the effect on its characteristics causes some difference in the actual and obtained values. Let us see the various errors and characteristics of a current transformer.
Errors in Current Transformer :
Before learning about errors in the current transformer. Let us see the current and turn ratio of a current transformer.
Turn Ratio (n) :
For a current transformer, if N1 and N2 are the number of turns in the primary and secondary windings. Then turn ratio is defined as the ratio of the number of secondary turns N2 to the primary turns N1.
Actual Current Ratio (R) :
It is the ratio of the magnitude of current in the primary to the secondary windings. It is denoted by 'R'. The actual current ratio is the transformation ratio of a current transformer.
Nominal Current Ratio (Kn) :
The nominal current ratio of a current transformer can be obtained from the data mentioned in the nameplate details. It is the ratio of the rated primary winding current to the secondary winding current.
The relation between the actual and nominal current ratio is given by the 'Ratio Correction Factor (RCF)'.
Owing to this turn, actual, and nominal ratios of a current transformer. There are two types of errors in a current transformer. They are ratio error and phase angle error.
Ratio Error :
The ratio error of a current transformer is due to a change in the actual current ratio from the turn ratio. We know that for a current transformer the current ratio must be equal to the turn ratio i.e., I1/I2 = N2/N1. But due to magnetizing and cross loss components of the primary winding current and power factor of the seconding winding. The current ratio I1/I2 will differ from the turn ratio N2/N1.
Thus the actual current ratio will not be constant and depends upon the load current, and power factor of the load or burden connected to the secondary. Due to this change in the actual current ratio, the current in the primary cannot be determined exactly and causes an error called ratio error. The formula for percentage ratio error is given as,
Phase Angle Error :
In practice, the secondary current of the CT must be in exact phase opposition with the primary current i.e., exactly by 180 phase difference. At the time of power measurement, there exists a difference in the phase angle between primary and secondary currents.
This is due to fact that the primary current has to supply core loss and magnetizing components of the CT for which it losses some phase angle. Due to this, the secondary current wouldn't be in exact phase opposition.
This difference or loss in phase angle causes an error called 'Phase Error or Phase Angle Error' denoted by angle θ. The phase angle error can understand by the below phasor diagram of a current transformer.
Where,- Ip = Primary current
- Is = Secondary current
- n = Turn ratio
- Io = Excitation current
- Ic = Core loss component
- Im = magnetising component
- Ep = Primary induced EMF
- Es = Secondary induced EMF
- Φ = Flux develop
- θ = Phase angle error
- α = Burden Angle
- β = Angle between flux and excitation current.
In the above phasor diagram, by taking flux as the reference. If load connected is to be lagging power factor. The secondary current Is lags behind the secondary emf Es.
The primary has to supply excitation current components i.e., Im and Ic. The secondary current can be referred to as primary by multiplying with the turns ratio i.e., nIs. The vector sum of nIs and Io gives the primary current. The phase angle error is given by,
In practice, most of the loads (relays or instrument or pilot lights) connected across secondary are inductive type. For inductive, δ is positive and very small. Therefore, sine δ ≈ 0 and cos δ ≈ 1. By substituting in the above equation we get,
Characteristics of Current Transformer :
The characteristics of a current transformer are affected by various parameters like frequency, power factor, and load or burden.- Since the secondary of a current transformer is connected to a relay or other instruments. It affects the power factor of the secondary circuit. The power factor of secondary depends upon p.f. of burden connected to it. Due to this effect in p.f., it introduces errors in the transformers (ratio and phase error).
- Since the secondary current is directly proportional to the primary current. When the primary is supplied through low currents, most of the primary current component Ip will be taken for magnetizing Im and core loss Ic components. This causes more loss in the core, increasing the errors. Once the primary current is increased, the components Ic and Im are a significant part of Ip. Thereby decreasing the core loss and errors.
- The change in the burden on the secondary of a current transformer also affects its characteristics. The burden of a secondary is nothing but the value of volt-ampere connected. The increase in burden also increases the VA rating of the secondary. Due to this the secondary draws more current and induces more voltage. Thus, Ic and Im components of the primary current increase to balance the secondary increased current. Therefore, the errors of the instrument also increase.
- We know that the flux density of a machine depends upon its operating frequency. Thus variation in frequency also varies flux density. By reducing the Ic and Im the error also gets reduced.
Reduction of Errors in Current Transformer :
By Reducing Magnetising and Core Loss Components :
The errors seen above are mostly due to core loss and the magnetizing components of the primary current. In order to reduce Ic and Im, the magnetic core of a current transformer is built in such a way that,
- The material used to build must be highly permeable.
- The reluctance of the core material should low as possible.
- By maintaining low flux density and a large cross-section of the core.
By Reducing Winding Resistance and Leakage Reactance :
The ratio and phase error of a current transformer also depends upon voltage drop due to winding resistance, and leakage reactance due to leakage flux. By using high cross-sectioned conductors the resistance of the winding can be reduced. In order to reduce flux leakage, co-axially placed HV and LV windings are used by increasing their mutual coupling.
Turn Compensation :
By decreasing the number of secondary turns on a current transformer, the actual or transformation ratio decreases. So that when the burden on the secondary is connected, it can be made equal to the nominal ratio. Thereby reducing the ratio errors in the current transformer.