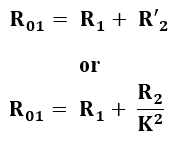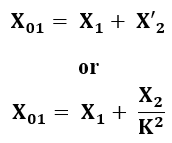An induction motor is an asynchronous motor i.e., its speed change with a change in load. It always runs on a lagging power factor. The principle of working of an induction motor to similar to the transformer i.e., electromagnetic induction.
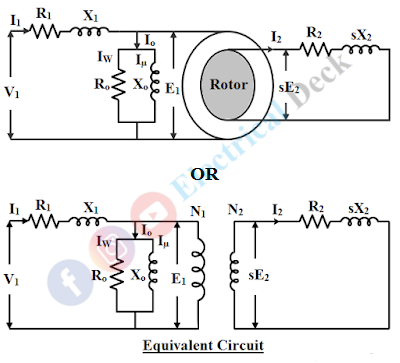
The equivalent circuit of an induction motor is similar to a transformer equivalent circuit because the energy is transferred from stator to rotor is essential as a transformer operation from primary to the secondary winding.
An equivalent circuit enables the performance characteristics of the induction motor. The data obtained from the equivalent circuit can be used to calculate efficiency, torque, losses, rotor output, etc. All per phase quantities are used in representing the equivalent circuit.
Equivalent Circuit of induction Motor :
The various parameters used for developing the equivalent circuit of an induction motor are,- R1 & X1 : Stator winding resistance and leakage reactance.
- R2 & X2 : Rotor winding resistance and leakage reactance at standstill (i.e., s = 1).
- sX2 : Rotor leakage reactance at slip s (under running condition).
- Ro : No-load branch resistance and it carries working component (Iw) of no-load current Io account for the losses on no-load.
- Xo : No-load branch reactance and it carries magnetizing component (Iµ) of no-load to produce the flux.
- E1 and sE2 : Stator induced emf and rotor induced emf at slip s.
From the above parameters, the equivalent circuit of an induction motor can be drawn as shown below,
let us consider the actual rotor circuit of the motor.
From the above diagram, the rotor current I2 is given by,
Here we know that the rotor input, P2 is the sum of rotor copper losses Pc and mechanical power developed Pm. Thus it is possible to represent the electrical equivalent of mechanical power developed as follows,
To show the equivalent mechanical load (mechanical power conversion) in the rotor circuit. The motor equivalent circuit can be modified as,
Now transfer the rotor side parameters to the stator side. While shifting the rotor side parameters towards the stator side we have to divide it by the value "K" (Where K = Ratio of the effective rotor to stator turns per phase) except the rotor current where it is multiplied by "K". When the rotor parameters are shifted they can be represented as,
- R'2 = Rotor resistance referred to the stator.
- X'2 = Rotor reactance referred to the stator.
- E'2 = Rotor induced e.m.f. referred to the stator.
- I'2 = Rotor current referred to the stator.
- R'L = Rotor equivalent mechanical load referred to the stator.
The equivalent circuit can be further modified as shown below, and it is known as the Exact Equivalent Circuit as referred to as the stator.
Where,
Therefore, the approximate equivalent circuit is obtained by shifting the shunt branch (consists of R01 & X01) to the supply terminals as shown in the below figure. This simplification will enable easy calculations.
Therefore, the total resistance referred to the stator side is,
Similarly, the total reactance referred to the stator side is,
Calculation of Rotor Output and Torque Using the Equivalent Circuit :
From the equivalent circuit, we can derive expressions for torque T, and rotor output power Po of the motor.
From the above diagram, the power input Pi to the rotor is given by,
We can write,
Pi = SPi + Pi - SPi (by adding and subtracting SPi)
Pi = SPi + (1 – S)Pi
The above expression shows that the rotor input power, Pi is the sum of voltage drop in the rotor circuit due to its resistance as SPi and the equivalent resistance representing mechanical load (1 - S)Pi. From the above, the rotor output Po is given by,
We know that rotor current I2,
By substituting the value of I2 in equation (1) we get,
We know that the rotating magnetic field of the induction motor produced by the stator winding rotates at synchronous speed Ns. Then the torque applied on the rotor due to the stator rotating magnetic field will be T. Now, the power transferred from stator to rotor is given by,
Equating the equations 2 & 3 we get,
Therefore, the torque equation is derived from the equivalent circuit and various performance calculations can be performed from the above equations.
