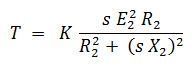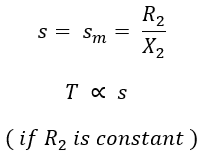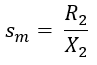We know that the induction motor is an asynchronous motor (i.e., not a constant speed motor). Its speed changes with a change in the load connected to it. As the load on the motor increases the slip of the motor increases. This makes the motor increase the amount of torque produced in order to meet the load demand.
Hence, to study the behavior induction motor. It is important to know the torque-slip characteristics of an induction motor. The curve drawn plotted between torque against slip is called torque-slip characteristics of the induction motor. We know that from the torque equation of induction motor the expression for the torque is,
Torque-Slip Characteristics of Induction Motor :
Now, let us evaluate the value of torque at different values of slip in the range from 0 to 1.
At Low Values of Slip :
Starting from zero, when slip s = 0, rotor speed N is equal to synchronous speed Ns (N = Ns i.e., the rotor speed is equal to the speed of the rotating magnetic field). At this condition, the net torque produced on the rotor is zero. Hence, the motor cannot run at synchronous speed.
- When the speed of the rotor is very near to synchronous speed (but not equal to synchronous speed) the value of slip will be slightly greater than the zero i.e., a very low value of slip, s. Then, the term (sX2)2 is very small and can be neglected when compared to R22.
- When slip increases due to an increase in load, the speed decreases. This in turn increases torque and becomes a maximum Tm. As the torque produced is maximum (T = Tm) the value of slip will also be maximum (s = sm). The torque produced by the induction motor is maximum when rotor resistance R2 is equal to rotor reactance X2.
The value at which torque becomes maximum is known as pull-out or breakdown torque.
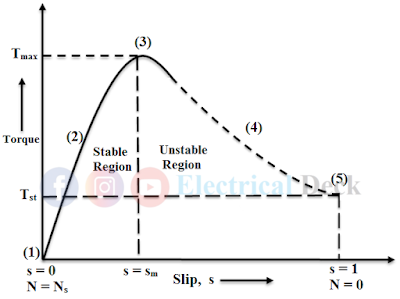
- Hence for low values of slip, the torque-slip curve obtained will be approximately a straight line as shown in the below figure (from 1 to 3).
Here, we can notice that if the value of slip increases (due to an increase in load demand) the torque produced increases to meet the load demand. Therefore, the torque is directly proportional to slip until the motor attains its maximum torque and the operation of the motor in this region is stable.
At High Values of Slip :
When the slip of the motor increases beyond its maximum value, then the motor is said to be running at high values of slip.- When slip is further increases beyond s = sm, then the resistance of the rotor R22 is very small as compared to the reactance of the rotor (sX2)2 and it can be neglected.
Here the torque decreases as the slip increases. The obtained torque-slip curve at this condition will be a rectangular hyperbola (from 3 to 5) as shown in the below figure.
- If the value of the slip is equal to one (s = 1), the speed will be zero. Therefore, the motor will remains stationary. Hence the corresponding torque is nothing but starting torque. i.e., T = Tst (when s = 1)
From the above, we can say that at high values of slip (when the slip is greater than its maximum value i.e., s > sm). The torque produced is inversely proportional to the slip due to this there will be a drop in rotor speed, and the motor will operate in the unstable region.
The region from s = 0 to s = sm is called the operating region for the induction motor because if the load is increased beyond s = sm, then torque decreases and the motor will stop.
Effect of Rotor Resistance on Torque-slip Curve :
In a slip-ring induction motor, it is possible to add external resistance in series with the rotor through slip rings. This is used to control the starting torque developed by the motor. Let, R2 = rotor resistance per phase, then the torque is given by,
At standstill, the rotor reactance phase, X2 will remain constant, since it is fixed by the design of the rotor.
- When no external resistance is inserted in the rotor circuit. Maximum torque is developed at,
- Now if rotor resistance is increased (inserting external resistance in the rotor circuit) from R2 to R'2. The magnitude of the maximum torque, Tmax remains unchanged but the slip for maximum torque is,
- As rotor resistance is increased from R'2 to R''2, and so on, as shown below that Tmax remains the same but starting torque increases.
- At sm = 1 i.e., when R2 = X2, the motor will develop maximum torque at the instant of starting. This is represented by point 'A' in the below figure.
