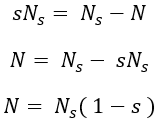Why induction motor can not run at synchronous speed?
When the supply is given to the induction motor the field winding set-ups a magnetic field rotating at synchronous speed Ns (i.e., Ns = 120f/number of poles), and the field is known as a rotating magnetic field.
As the rotor is rotating in this magnetic field, the magnitude of rotor-induced currents will be proportional to the relative speed between the stator rotating field and rotor speed and this current always lags with the main field current. Thus it is difficult to maintain synchronism between the main field flux speed and rotor rotating speed.
Let us assume that the rotor rotates at synchronous speed, so the emf induced in the rotor conductors would become zero and consequently, there is no torque on the rotor causing the rotor to fail back in speed. Once the rotor falls back in speed, the relative speed increases, and again rotor picks up the speed.
But due to the inertia of the rotor, this does not happen in practice and the rotor continues to rotate with a speed slightly less than the synchronous speed of the rotating field. Therefore, an induction motor will always rotate at a speed N less than the speed of synchronous speed Ns (speed of rotating magnetic field).
What is Slip in Induction Motor?
We have seen that there will be a difference in the speed of the rotating magnetic field and rotor rotating speed. This difference in speed expressed by the percentage of synchronous speed Ns is known as the slip of the motor. Therefore, The slip 's' is defined as the difference between the speed of the main magnetic field (Ns) and the rotor rotating speed (N). Thus slip,
From the above equation, the actual speed of the motor can be expressed as,
From the equation of slip s, it may be noticed that the relative speed or slip speed (Ns - N) of the rotor and rotating magnetic field is directly proportional to the slip.- At starting or standstill position of the rotor, N = 0. At this condition the slip s = 1, and this is the maximum value of slip.
- The value of slip cannot be zero because when s = 0, N = Ns, thus torque produced will be zero. This can be understood by the torque-slip characteristics of the induction motor.
- At no-load slip is very low (near to 0) about 1% and at full load, it is about 3-5%. The variation in slip and therefore speed, from no-load to full load is very small. Thus we can say a 3-phase induction motor is also a constant speed motor.
Effect of Slip on Induction Motor Parameters :
Rotor Frequency :
In an induction motor, the relation between synchronous speed, supply frequency, and the number of stator poles is given by,
When the rotor rotates at a speed 'N' then the rotor conductor cut the rotating magnetic field at the relative speed i.e., Ns - N. The frequency of the rotor induced emf or current 'fr' can be expressed as,
Dividing equation 2 by 1, we get,
Therefore, fr = s f at the running condition. So rotor frequency in running condition is slip times the supply frequency.- Suppose, at starting, N = 0 and slip = 1, hence fr = f.
- Under the normal running condition, the rotor frequency is very small as the slip is very small.
Rotor Induced EMF :
When the rotor is stationary or at standstill (N = 0) i.e., slip = 1, the emf induced in the rotor is maximum. This is due to the rate of cutting the flux by the rotor is maximum as the relative speed between the rotor and rotating magnetic field is maximum. Let E2 be the rotor-induced emf per phase at standstill.
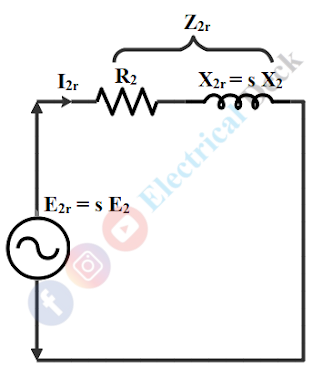
As the speed of the rotor increases, the relative speed decreases. This reduces the magnitude of induced emf in the rotor and proportionality. The relative speed is 'Ns - N' rpm when the motor is running at speed 'N' rpm. Let E2r be the rotor induced emf per phase under running conditions.
Dividing equation 2 by 1, we get,
Therefore, rotor-induced EMF under running conditions will be slip times the rotor-induced EMF at standstill.
Rotor Reactance :
The rotor reactance depends upon the frequency. We know that at slip s, the frequency of the rotor induced emf is given by fs = s f.
At the standstill (s = 1) condition the frequency of the rotor is given to be fr = f. As the rotor winding comprises inductance, the formula for rotor inductive reactance is given by X2 = 2π f L2. Where L2 is the per phase inductance of the rotor. Therefore, under standstill condition, the rotor per phase reactance X2 is given by,
similarly, under running condition (s ≠ 1) condition the frequency of the rotor is given to be fr = sf. Therefore, the per-phase rotor reactance X2r under running conditions is given by,
Therefore, rotor reactance under the running condition will be slip times the rotor reactance at standstill.
Rotor Resistance :
The resistance of the rotor is independent of frequency and hence rotor resistance remains the same as R2 Ω per phase at standstill as well as in the running condition.
Rotor Impedance :
The expression for rotor impedance is obtained by combining rotor resistance and rotor reactance. Therefore, the per-phase rotor impedance Z2 at standstill is given by,
Similarly, under the running condition,
Rotor Current & Power Factor :
From the equations of rotor resistance, impedance, and power factor under the standstill and running condition. The equivalent circuit of the rotor at standstill can be drawn as shown below.
From the equivalent circuit, the standstill rotor current I2 and power factor cos Φ2 is given as,
Similarly, under the running condition, the equivalent circuit is shown below.
From the equivalent circuit, the rotor current I2r and power factor cos Φ2r under running condition is given as,
